
Abb. 1: Kollision zweier Wellen
Optimierung und Variationsrechnung. Jeder Mensch verfolgt Optimierungsstrategien, wenn er etwa versucht günstig einzukaufen. Schon hier ist zu fragen, was optimal bedeutet. Erst recht wenn Optimierungsprobleme unübersichtlich werden, helfen mathematische Methoden zur Präzisierung des Optimalitätsbegriffs als auch zum Auffinden optimaler Lösungen. Zu solch komplizierten Problemen gehören in Köln der Entwurf von tragfähigen Kränen, die selbst möglichst wenig wiegen sollen, das Design von Körpern minimalen Strömungswiderstandes oder von Messerklingen, die möglichst gut schneiden, die Optimierung von Fertigungsprozessen und Nahverkehrsfahrplänen oder die Routenplanung von Spediteuren. Je nachdem ob endlich oder unendlich viele Varianten zu optimieren sind, spricht man von diskreter oder kontinuierlicher Optimierung. (Bachem, Kawohl)
Differentialgleichungen beschreiben räumliche
und zeitliche Ausbreitungsvorgänge wie etwa das Wetter, oder das in
Köln studierte Versickern von Schadstoffen im Boden und das Erstarren
von Stahl in einer Stranggußanlage. Sie lassen sich oft nur näherungsweise
lösen, und die mathematischen Gleichungen haben oft viele Lösungen,
von denen nur einige problemrelevant sind. Differentialgleichungen beschreiben
auch die Ausbreitung von Epidemien, Wellen, Strahlen und Kraftfeldern;
und deren genauer Beschreibung verdanken wir es beispielsweise, daß
der Computertomograph aus physikalischen Messungen und Zahlenkolonnen ein
Bild berechnet, welches den Zustand des Patienten annähernd korrekt
widergibt. Je mehr physikalisch-chemische Effekte dabei mit berücksichtigt
werden sollen, desto komplizierter werden die Gleichungen und desto mehr
mathematisches Geschick erfordert die Lösungsberechnung. (Kawohl,
Küpper, Lange)

Abb. 1: Kollision zweier Wellen
Die Differentialgeometrie hat ihren Ursprung in der Untersuchung von Kurven und Flächen und der mathematischen Modellierung des physikalischen Raumes. Die grundlegenden Begriffe der Differentialgeometrie sind die der "Mannigfaltigkeit", als dem Raum der Geometrie und Physik, und der "Krümmung". Auch in der jüngsten Zeit stellt die Differentialgeometrie der Physik fundamentale Modelle zur Verfügung. Dadurch gilt sie als eine wesentliche Schnittstelle zwischen Mathematik (gedanklichen Konstrukten) und Physik (erlebbarer Welt). Ein Kölner Schwerpunkt ist die Untermannigfaltigkeitsgeometrie, die moderne Version der Flächentheorie, z.B: Untermannigfaltigkeiten in komplexen Raumformen und symmetrischen Räumen, Immersierbarkeit hyperbolischer Räume in euklidischen mit möglichst kleiner Codimension, Zerlegbarkeit isometrischer Immersionen. (Henke, Reckziegel, Thorbergsson)
![[Maple Plot]](bianchi.gif)
Abb. 2: Die Bianchi-Fläche, eine Fläche
mit konstanter negativer Krümmung und einer Schar ebener Krümmungslinien
Singularitäten. Wenn man eine Kurve in der Ebene oder eine Fläche im Raume durch eine Gleichung beschreibt, fallen Störungen des glatten Verlaufs auf. Die betroffenen Stellen heißen Singularitäten. Sie erscheinen beispielsweise in der Optik als besonders helle Brennpunkte der Kaustiken (Brennflächen). Um die Gestalt der Singularitäten zu erfassen, werden Methoden der Geometrie und Topologie, der Analysis und der Algebra herangezogen. Dabei treten viele interessante Beziehungen auf, z.B. zu Knoten, zu regelmäßigen Polyedern, zur Gruppentheorie und zur kommutativen Algebra. Singularitäten werden von uns anhand ihrer Auflösung studiert. Darunter versteht man eine algebraische Methode, deren geometrische Deutung im Falle von Flächensingularitäten darauf hinaus läuft, jeden singulären Punkt so durch eine Kurve zu ersetzen, daß eine überall glatte Fläche entsteht. (Lamotke)
Algebraische Geometrie. Der klassische Gegenstand der Algebraischen Geometrie sind geometrische Gebilde, die durch algebraische Gleichungen beschrieben werden. Man kann damit zum Beispiel verstehen, wann und in welcher Weise 3 Gleichungen vierten Grades in 5 Variablen eine Fläche beschreiben. Umgekehrt kann man mit dieser Theorie auch algebraische Objekte, ja sogar die Zahlen selbst, in geometrischer Weise behandeln. Durch den damit verbundenen Übergang zu neuen Zahlenbereichen, den sogenannten endlichen Körpern, gab es unerwartete Anwendungen in der Codierungstheorie, d.h. in der Verschlüsselung sensibler Daten. In Köln werden diskrete Invarianten (Kohomologie, K-Theorie und Algebraische Zykel) und stetige Parameter (Modulräume) studiert, sowie Anwendungen auf zahlentheoretische Fragen. (Jannsen, Lamotke, Rapoport)
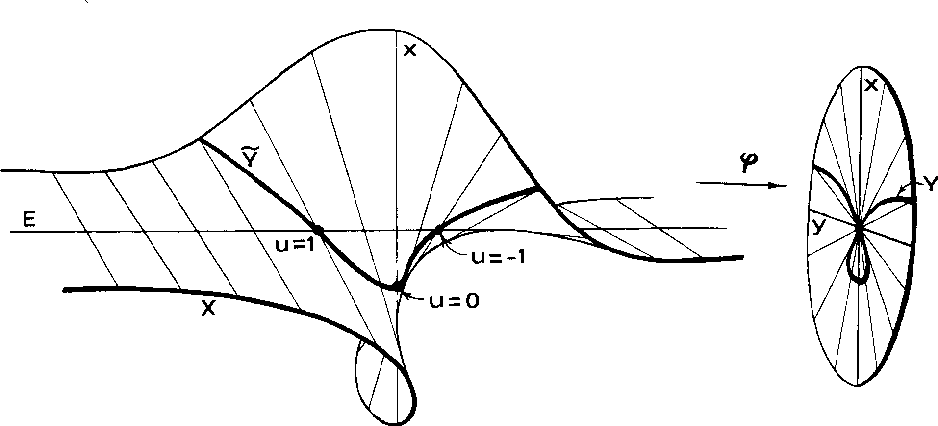
Abb. 3: Auflösung einer Singularität
In der Verzweigungstheorie analysiert man parameterabhängige Gleichungen vor allem in Hinblick auf qualitative Änderungen der Lösungsstruktur und auf Stabilitätswechsel bei Durchlaufen kritischer Parameter. Schwerpunktmäßig wird in Köln bearbeitet: Verzweigung aus dem wesentlichen Spektrum mit Anwendungen in der mathematischen Physik (nichtlineare Schrödinger- und Klein-Gordon-Gleichungen). Innerhalb des DFG-Schwerpunktes "Dynamik" werden klassische Konzepte auf nichtglatte Dynamische Systeme übertragen und zur Modellierung von Reib- oder Stoßvorgängen herangezogen. Im Graduiertenkolleg "Scientific Computing" werden epileptische Vorgänge mit Hilfe von großen Systemen von Funktionaldifferentialgleichungen modelliert. Ein von der Stiftung Volkswagen gefördertes Projekt mit russischen Physikern befaßt sich mit der Modellierung der optischen Signalübertragungen. (Küpper)
Gegenstand der diskreten Mathematik sind strukturierte endliche Mengen. Aus der traditionellen Kombinatorik, die sich mit allgemeinen Anzahl- und Existenzproblemen befaßte, hat sich mit wachsender Rechnerkapazität eine praxisorientierte Disziplin entwickelt, deren Resultate zum Beispiel in der Verkehrsplanung oder in der Unternehmensforschung von großer Bedeutung sind. Zur effizienten Lösung konkreter Optimierungsprobleme braucht man schnelle Algorithmen, deren Entwicklung ohne fundierte Kenntnis der probleminternen diskreten Strukturen nicht möglich ist. In Köln werden insbesondere Probleme der kombinatorischen Geometrie und der Graphentheorie untersucht. (Armbrust, Bachem)
Die Stochastik, also die mathematische Theorie zufälligen Geschehens, hat einen vielfältigen Anwendungshintergrund. Zu ihren historischen Wurzeln gehören so unterschiedliche Probleme wie die Frage nach Gewinnstrategien bei Glücksspielen (N. Bernoulli, P.S. Laplace), die Ermittlung eines "korrekten" Meßwertes aus einer fehlerbehafteten Meßreihe (C.F. Gauß) oder die Bestimmung des Wertes einer Leibrentenzusage (C. u. L. Huygens). Diese drei Problemkreise stehen stellvertretend für die beiden wichtigsten Teilgebiete der Stochastik, die Wahrscheinlichkeitstheorie und die mathematische Statistik, sowie für eines ihrer zentralen Anwendungsfelder, die Versicherungsmathematik. Nachdem die Mathematische Statistik in Köln mehr als 30 Jahre herausragend vertreten war, liegen die Schwerpunkte in der Kölner Stochastik derzeit in den Bereichen Wahrscheinlichkeitstheorie und Versicherungsmathematik. (Landers, Milbrodt)
Liesche und Algebraische Gruppen. Mathematische Objekte wie algebraische Gleichungen oder auch Differentialgleichungen können Symmetrien besitzen. Die Gesamtheit der Transformationen, die das mathematische Objekt invariant lassen, bilden die Symmetriegruppe des Objekts. Bei einer algebraischen Gleichung verrät sie, ob die Lösung der Gleichung nur in Wurzeln und Grundoperationen ausgedrückt werden kann. Die entsprechende Frage für Differentialgleichungen (und Integrale statt Wurzeln) führte Lie zu den sog. Liegruppen, bei deren Untersuchungen analytische Methoden eingesetzt werden und die in vielen Gebieten der Mathematik und Physik von großer Wichtigkeit sind. In Köln werden assoziierte homogene Räume und - vor allem beim algebraischen Analogon, den algebraischen Gruppen - die zugehörigen Darstellungen und algebraischen Varietäten untersucht. (Thorbergsson, Rapoport)
Algebra und Zahlentheorie. Die Algebra hat
ihren Ursprung in der Untersuchung von Rechengesetzen und mathematischen
Gleichungen und hat durch fortgesetzte Abstraktion Theorien entwickelt,
die die Behandlung kompliziertester Sachverhalte ermöglicht. Sie gehört
damit zum Rüstzeug der Mathematiker selbst und dringt am wenigsten
nach außen, obwohl die Computeralgebra beachtliche Anwendungen hat.
Gegenstand der Zahlentheorie sind die Zahlen selbst. Sie ist geprägt
durch tiefliegende Vermutungen (wie die von Riemann), deren Lösung
oft die Entwicklung neuer starker Methoden stimulierte und erforderte (wie
jüngst beim Beweis der Fermat-Vermutung). Viele Fragen, z.B. Klassifikationsansätze
in der Topologie, führen auf zahlentheoretische Probleme. In Köln
werden u.a. Transzendenzfragen, Galoisdarstellungen und Zetafunktionen
untersucht. (Armbrust, Bundschuh, Jannsen, Rapoport)
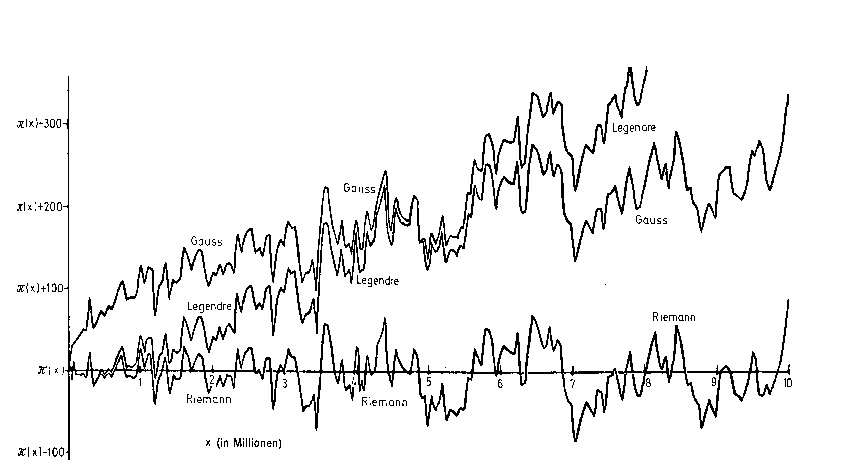
Abb. 4: Die Primzahlfunktion ¶(x)
Zur Forschungstätigkeit des Instituts gehört neben der Publikation in internationalen Fachzeitschriften auch die Durchführung von und Beteiligung an zahlreichen Tagungen und Sommerschulen, Mitherausgabe von Fachzeitschriften "Duke Math. J." (Rapoport) "Math. Nachrichten" (Jannsen, Kawohl), "Jahresber. der DMV" (Kawohl), und die Gutachtertätigkeit für DFG, DAAD, NSF, AvH und zahllose internationale Fachzeitschriften.
Es gibt enge personelle Verknüpfungen des Instituts mit dem Zentrum für paralleles Rechnen, einer zentralen Einrichtung der Universität, die zum großen Teil Forschungs- und Entwicklungsaufträge für Industriefirmen durchführt; ferner zu anderen Instituten der Universität (z.B. Versicherungswissenschaft), zur DLR (Bachem), zur Ges. f. Math. u. Datenverarb. in St. Augustin (Trottenberg) und zum Max Planck Institut für Mathematik in Bonn (Rapoport). Engere Kontakte in Köln bestehen auch zu regionalen Versicherungsunternehmen, sowie zu den Firmen Bayer und Risk Consulting, die mit Dozenten sowie mit den apl. Professoren Brüll und Weyer unser Lehrangebot um Praktika, konkrete Examensthemen und Seminare bereichern. Die Absolventen unseres Instituts finden vorwiegend Arbeit im schulischen und akademischen Bereich, in der Industrie bei Software- und Unternehmensberatungsfirmen, bei Banken und Versicherungen.
Das Institut pflegt zahlreiche wissenschaftliche Kontakte sowohl zu internationalen Forschungszentren (z.B.: MSRI, Berkeley, IHES, Paris, RIMS, Kyoto und IAS, Princeton), zu namhaften ausländischen Universitäten (z.B.: Pisa, Paris, Tokyo, Los Angeles, Boston, New York, Prag) als auch zu Hochschulen in Entwicklungsländern.
Alle diese Kontakte werden im wesentlichen von Drittmittelgebern
(Europ. Gem., DFG, DAAD, Alexander von Humboldt Stiftung, VW, Hertz Stiftung)
finanziert, bisweilen über mehrere Jahre hinweg, wie beim EU Projekt
"Arithmetic Algebraic Geometry", an dem die Universitäten Straßburg,
Rennes, Paris, Barcelona, Padua, Cambridge und Durham beteiligt sind.
Quellenangaben Abbildungen