Forschungsinteressen
Mathematische Biologie, Analysis, Partielle Differentialgleichungen, Variationsrechnung.
Unter anderem:
Parabolische "Vorwärts-Rückwärts" - Gleichungen und ihre Regularisierungen, z.B. in der Bildverarbeitung und bei Populationsmodellen:
In letzter Zeit sind vorwärts-rückwärts parabolische Gleichungen wieder mehr in das Interesse der Mathematiker gerückt. Derartige parabolische Probleme kommen in der Bildverarbeitung und in der Populationsdynamik vor.
Verwendet man zum Beispiel den sogenannten Zell-Potential Ansatz oder betrachtet man den parabolischen Limes eines Random walks auf einem zugrundeliegenden Gitter, so sieht man, dass Dichte-abhängige Modelle für die Bewegungen von Populationen in der Regel durch Gleichungen der Form
![]()
oder
![]()
beschrieben werden (vgl. hierzu zum Beispiel Arbeiten von D. G. Aronson, J. D. Murray & D. S. Cohen, sowie
M. E. Gurtin & R. C. MacCamy). Abhängig von den Funktionen q bzw. Q können diese Gleichungen vorwärts-rückwärts parabolische Probleme darstellen.
In der Bildverarbeitung haben Perona und Malik die Gleichung
![]()
mit einer Diffusionsfunktion q, die das Vorzeichen genau einmal ändern darf, als ein Modell zum Entrauschen eines gegebenen Anfangbildes vorgeschlagen. Numerische Berechnungen haben gezeigt, dass diese Gleichung den gewünschten Effekt eines entrauschten Bildes liefert. Die Diffusionsgleichungen sind jedoch hochgradig nichtlinear und enthalten als Spezialfälle äußerst schwierige Teilprobleme und eine allgemeine Existenztheorie ist nicht gegeben. Daher sind unterschiedliche Regularisierungen dieser Modelle eingeführt und vorgeschlagen worden, die es ermöglichen, Aussagen über das qualitative Verhalten der Lösungen der approximativen Modelle zu machen.
Literatur hierzu:
K. J. Painter, D. Horstmann und H. G. Othmer: "Localization in Lattice and Continuum Models of Reinforced Random Walks", Applied Mathematics Letters Vol. 16 (3), Seiten 375 - 381, 2003.
D. Horstmann, K. J. Painter und H. G. Othmer: "Aggregation under local reinforcement: From lattice to continuum", European Journal of Applied Mathematics Vol. 15, Seiten 545 - 576, 2004.
D. Horstmann: "On some cross-diffusion models in population dynamics and their connections to well-posed filters in signal enhancement processes", IMA J. Appl. Math. Vol. 70, Seiten 386 - 399, 2005.
D. Horstmann und B. Schweizer: "A free boundary characterization of measure-valued solutions for forward-backward diffusion", Advances in Differential Equations, Vol. 13, Seiten 201-227, 2008
Qualitatives Verhalten von Lösungen parabolischer Systeme partieller Differentialgleichungen mit negativer Kreuzdiffusion, z.B. Chemotaxis-Gleichungen:
Chemotaxis, gerichtete Bewegung von freibeweglichen Organismen (Bakterien, Algen, bestimmte Pilze) und Gameten (Moose, Farne, Grün- und Braunalgen) deren Richtung durch chemische Stoffe und den Konzentrationsgradienten im diese umgebenden Medium bestimmt wird. Positive Chemotaxis liegt vor, wenn die Bewegung zur Reizquelle hin gerichtet ist. Negative Chemotaxis findet statt, wenn sich Organismen von dieser entfernen. Saprophytische und parasitische Bakterien und Pilze nutzen Chemotaxis, um zu ihren Nahrungsquellen bzw. Wirten zu gelangen, wohingegen Geschlechtszellen Lockstoffe abgeben, um Partner zu finden.
So ist zum Beispiel im Entwicklungsgang zellulärer Schleim-Pilze zu beobachten, dass nach einer Vermehrungsphase der aus den Pilzsporen entstandenen Amöben eine Aggregation stattfindet. Diese wird bei einigen Pilzarten durch die Abgabe eines chemischen Stoffes durch eine sogenannte Gründerzelle ausgelöst. Die übrigen Amöben scharen sich in der nachfolgenden Zeit um diese Gründerzelle. 1970 haben E. F. Keller und L. A. Segel das nachstehende Modell vorgestellt, das heutzutage oft als das "klassische" Chemotaxis Modell bezeichnet wird:
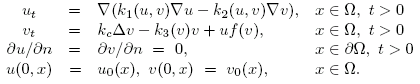
Für gewisse Anfangsdaten explodieren die Lösungen eines diesen Vorgang beschreibenden mathematischen Modells. Es stellen sich hierbei die Fragen, in welcher Form diese Explosion stattfindet und welche Voraussetzungen das Explosionsverhalten der Lösungen beeinflussen.
Positives chemotaktisches Verhalten lässt sich zum Beispiel dadurch nachweisen, dass man eine mit einer Nährlösung gefüllte Kapillare in eine Agarschale hält, in der sich eine Bakterien Population befindet (z.B. in eine E. coli Population). Die Bakterien werden sich um die Spitze der Kapillare versammeln und in Form von Bakterien-Verbänden die Kapillare der stärker werdenden Konzentration der Nährlösung hoch wandern.
Will man eine solches Verhalten mathematisch beschreiben, so korrespondiert die Formation der Bakterien-Verbände mit der Existenz von "Traveling wave"-Lösungen für das zugrundeliegende Chemotaxis Modell. In der Tat ist es so, dass es Versionen des "klassischen" Chemotaxis Modells gibt, für die Existenz von "Traveling wave" Lösungen nachweisbar ist.
Hierbei bildet sich bei der die Populationsdichte beschreibenden Funktion aufgrund der durch die Gleichungen implizierten Massenerhaltung ein wandernder Puls, während die die Chemikalie beschreibende Funktion eine Front ausbildet.
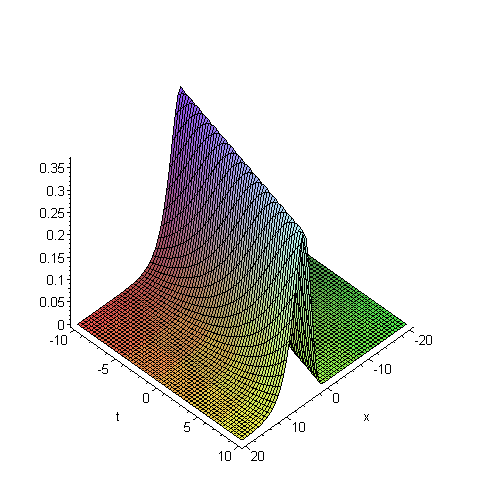
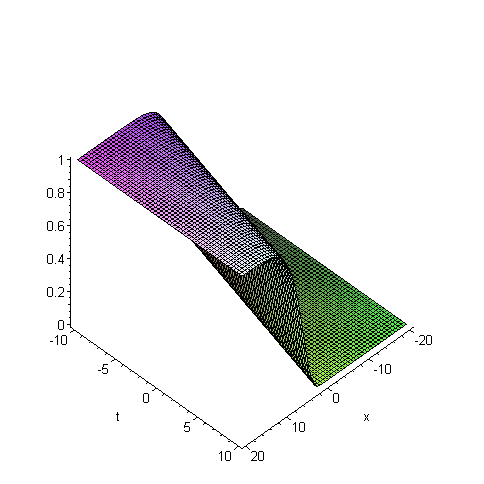
Ausgewählte Literaturhinweise hierzu:
D. Horstmann: "From 1970 until present: The Keller-Segel model in chemotaxis and its consequences I", Jahresbericht der DMV Vol. 105 (3), Seiten 103 - 165, 2003.
D. Horstmann: "From 1970 until present: The Keller-Segel model in chemotaxis and its consequences II", Jahresbericht der DMV Vol. 106 (2), Seiten 51 - 69, 2004.
D. Horstmann: "Generalizing Keller-Segel: Multi-species chemotaxis models with attraction and repulsion between competitive interacting species", Preprint 2009, zur Veröffentlichung eingereicht.
Vergleichssätze für Viskositätslösungen partieller Differentialgleichungen.
Lösungen elliptischer Gleichungen zweiter Ordnung erfüllen das sogenannte Maximumprinzip. Umgekehrt nennt man Funktionen, die ein entsprechendes Maximumprinzip erfüllen, Viskositätslösungen. Diese Definition einer Lösung für eine elliptische partielle Differentialgleichung setzt keine Differenzierbarkeit der zu betrachtenden Lösungen voraus. Es werden lediglich Stetigkeits- oder Halbstetigkeits-Forderungen an die Funktion gestellt. Daher ist dieser Lösungsbegriff wesentlich flexibler als die Definition klassischer Lösungen. Viskositätslösungen verhalten sich insbesondere bei Grenzübergängen einfacher und die Existenz von Viskositätslösungen ergibt sich allgemein mit der Perronschen Methode. Somit sind Vergleichsprinzipien in diesem Zusammenhang von besonderem Interesse.
Literatur hierzu:
D. Horstmann: "A note on comparison principles for viscosity solutions of fully nonlinear second order partial differential equations", Hokkaido Mathematical Journal Vol. 28-2, Seiten 315 - 331, 1999.
Optimierungsprobleme z.B.:
Das Newtonsche Problem des minimalen Strömungswiderstandes:
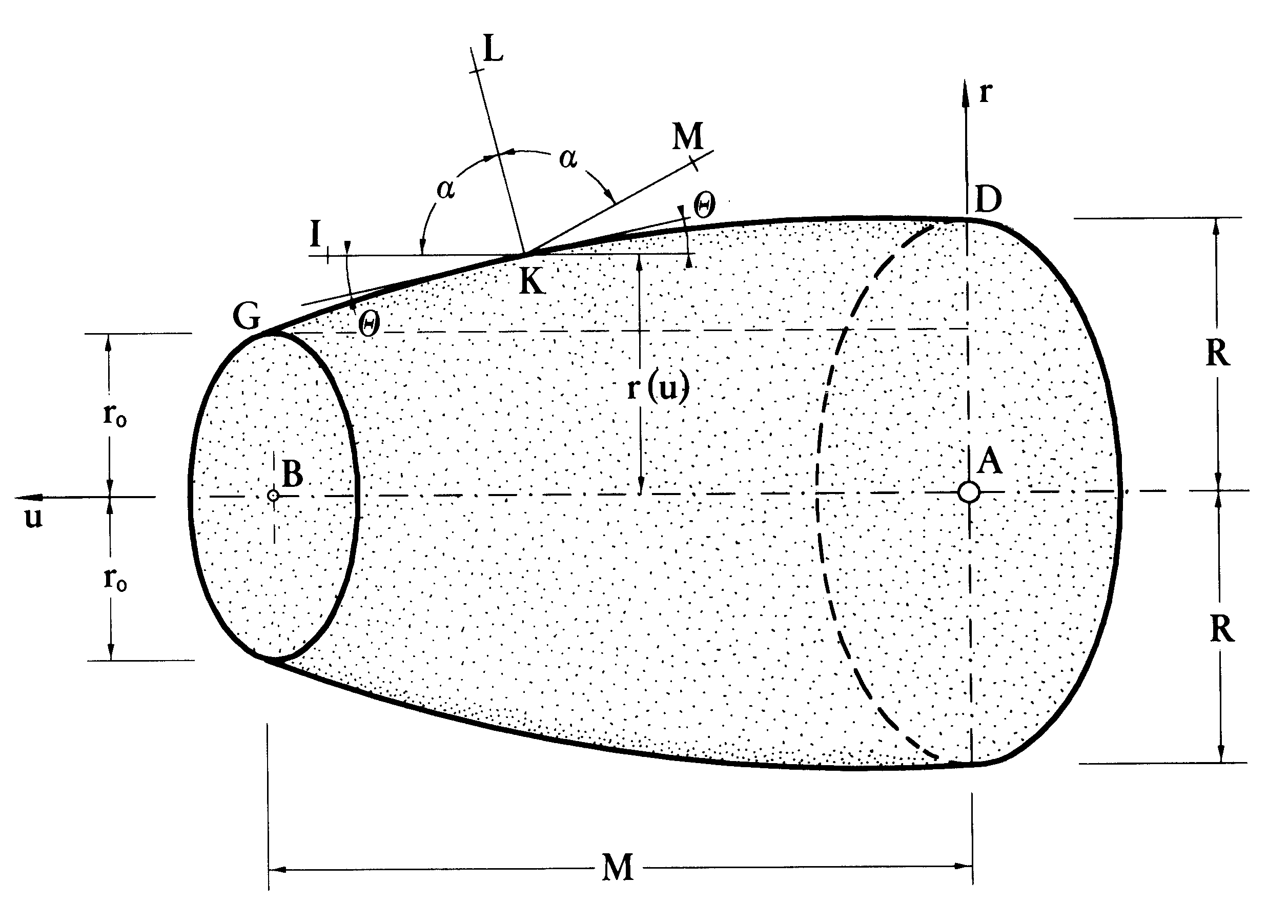
Gesucht ist ein Körper minimalen Strömungswiderstandes in einer verdünnten Partikelströmung. Die Modellierung dieses Problems führt auf ein nichtkonvexes, nichtkoerzitives Funktional, welches auf geeigneten Mengen von Körpern untersucht wird. Interessanterweise sind optimale Körper mit kreisförmigem Maximalquerschnitt nicht rotationssymmetrisch. Dies ändert sich bei der Berücksichtigung von Reibungseffekten.
Literatur hierzu:
D. Horstmann, B. Kawohl und P.Villaggio: "Newton's Aerodynamic Problem in the Presence of Friction" Nonlinear differ. equ. appl. (NoDEA) Vol. 9, Seiten 295 - 307, 2002.
Über konvexen Gebieten errichtete Kegel mit minimaler Oberfläche:
1955 formulierte Arne Pleijel in der Zeitschrift "Mathematica Scandinavica" das nachfolgende Problem:
"In einer Ebene E0 sei ein konvexer Bereich C gegeben. Es bezeichne ferner E eine zu E0 parallele Ebene und h ihren Abstand von E0. Man betrachtet den Kegel mit der Grundfläche C und einem Punkt P von E als Scheitel. Der Inhalt (des zwischen den Ebenen gelegenen Teils) der Mantelfläche des Kegels sei MP. Es ist leicht einzusehen, dass es einen und nur einen Punkt P=P0 in E gibt, für den MP sein Minimum erreicht. Ist C speziell ein Polygon, das einen Kreis so umschreibt, dass er von sämtlichen Seiten berührt wird, so fällt die orthogonale Projektion von P0 in den Mittelpunkt dieses Kreises. Was lässt sich für einen beliebig gegebenen konvexen Bereich C über die Lage der Projektion von P0 in Bezug auf C aussagen? Sind insbesondere die Grenzlagen dieser Projektionen für h à 0 und h à ∞ in einfacher Weise mit C verknüpft?"
Literatur hierzu:
M. Belloni, D. Horstmann und B. Kawohl: "Cones based on reflection symmetric convex polygons: Remarks on a problem by A. Pleijel", Forum Mathematicum Vol. 19, Seiten 933-953, 2007.