|

Traveling Waves
More precisely - traveling waves in a model of a
nonlinearly supported beam (like a suspension
bridge) or a plate. The motivation for the study of
this problem comes from an event that occurred on
February 9, 1938 on the Golden Gate Bridge in San
Francisco. The bridge engineer Russell G. Cone
described in his report that the suspended part of
the bridge displayed a wave-like motion (a wave
moving along the bridge) resembling cracking a
whip. Although it is more or less clear that the
cause of this was a strong gust wind blowing through
the bridge on that day, it has not been explained
exactly how the waves originated.
A mathematical model of such a bridge or a
suspended beam goes back to [2]. In its simplest
form the model describes the bridge by the equation
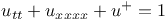 , , |
where 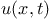 is
the deflection of the roadbed, the is
the deflection of the roadbed, the 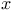 -axis
points in the direction along the bridge, -axis
points in the direction along the bridge, 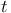 is time, the term is time, the term 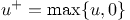 represents forces of the cables that apply only in
case the cables are tight
represents forces of the cables that apply only in
case the cables are tight 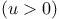 , but
not when they are loose. When looking for traveling
waves one searches for solutions , but
not when they are loose. When looking for traveling
waves one searches for solutions 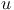 in
the special form in
the special form 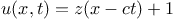 , where , where 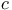 is a
given constant (the speed of the traveling
wave). is a
given constant (the speed of the traveling
wave).
In [1] we looked at a similar problem but made
several generalizations: the cables can apply some
force even if they are loose and the force is given
by some nonlinear function  , we work in more
space dimensions than just one - also in 2D and
3D. The equation then has the following form , we work in more
space dimensions than just one - also in 2D and
3D. The equation then has the following form
and we make the traveling wave
ansatz 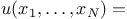 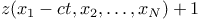 (in the direction of the (in the direction of the 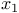 -axis). -axis).
The existence of traveling wave solutions of the
model was proved under some assumptions on the
nonlinear function  . Also, many numerical computations were
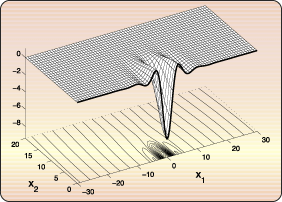
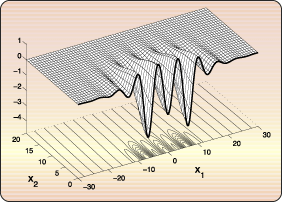
performed. They brought an evidence of existence of
multiple solutions with the same speed . Also, many numerical computations were
performed. They brought an evidence of existence of
multiple solutions with the same speed 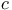 . Two
of them are shown in Figures 1 and
2. It was also observed that these waves have very
interesting interaction and stability properties. An
example of a collision of two waves is shown in the
movie in Figure 3. . Two
of them are shown in Figures 1 and
2. It was also observed that these waves have very
interesting interaction and stability properties. An
example of a collision of two waves is shown in the
movie in Figure 3.
References
| [1] |
J. Horak, P. J. McKenna,
Traveling waves in nonlinearly supported beams and
plates, Nonlinear Equations: Methods, Models and
Applications, Progress in Nonlin. Diff. Eq. Appl.,
vol. 54, Birkhäuser, Basel 2003,
197-215. |
| [2] |
P. J. McKenna, W. Walter,
Traveling waves in a suspension bridge, SIAM
J. Appl. Math. 50 (1990) 703-715. |
| [3] |
B. Breuer, J. Horak, P. J. McKenna,
M. Plum, A computer-assisted existence and multiplicity
proof for travelling waves in a nonlinearly supported
beam, J. of Differential Equations 224 (2006), no. 1,
60-97. |
 |
 |
|
|
 |

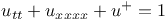 ,
,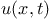 is
the deflection of the roadbed, the
is
the deflection of the roadbed, the 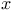 -axis
points in the direction along the bridge,
-axis
points in the direction along the bridge, 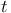 is time, the term
is time, the term 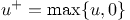 represents forces of the cables that apply only in
case the cables are tight
represents forces of the cables that apply only in
case the cables are tight 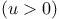 , but
not when they are loose. When looking for traveling
waves one searches for solutions
, but
not when they are loose. When looking for traveling
waves one searches for solutions 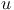 in
the special form
in
the special form 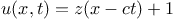 , where
, where 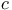 is a
given constant (the speed of the traveling
wave).
is a
given constant (the speed of the traveling
wave). , we work in more
space dimensions than just one - also in 2D and
3D. The equation then has the following form
, we work in more
space dimensions than just one - also in 2D and
3D. The equation then has the following form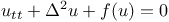
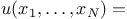
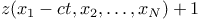 (in the direction of the
(in the direction of the 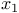 -axis).
-axis).