The main research focus of our group is Poisson geometry and geometries closely related to Poisson. As it is well known, Poisson geometry arises from the study of Classical Mechanics, similarly to Symplectic geometry, but with a stronger emphasis on understanding the symmetries of classical Hamiltonian systems. These invoke the notion of a Poisson bracket which, in the context of a manifold \(M\), corresponds to an anti-symmetric bracket \(\mathbb{R}\)-bilinear bracket \(\{\cdot,\cdot\}:C^\infty(M)\times C^\infty(M)\to C^\infty(M)\) which satisfies the Jacobi identity and the Leibniz rule. It turns out that an equivalent way to describe such a structure is to use a bivector field \(\pi\in\mathfrak{X}^2(M)=\Gamma(\bigwedge^2 TM)\) such that \([\pi,\pi]=0\), where this bracket is the Schouten-Nijenhuis bracket for multivector fields, a natural generalisation of the Lie bracket for vector fields.
The study of these Poisson manifolds yields many interesting properties from its links to symplectic geometry, Lie theory and foliation theory, allowing one to develop a theory that can simultaneously describe all these different aspects of geometry, whilst also providing fascinating insights into each of these seemingly disparate subjects. One such example is that every Poisson manifold has an associated foliation whose leaves are symplectic, as the following pictures show for well-known (duals of) Lie algebras.
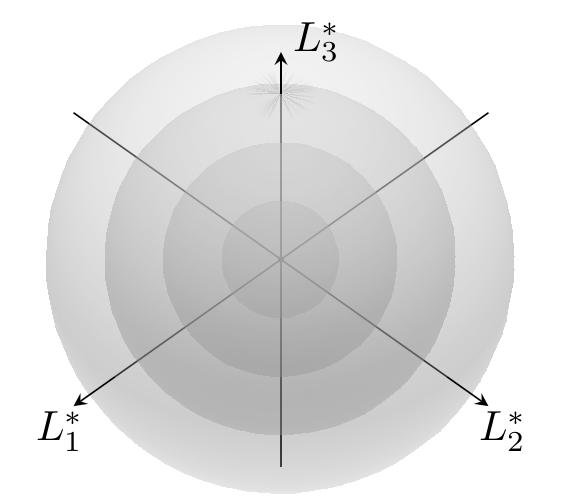
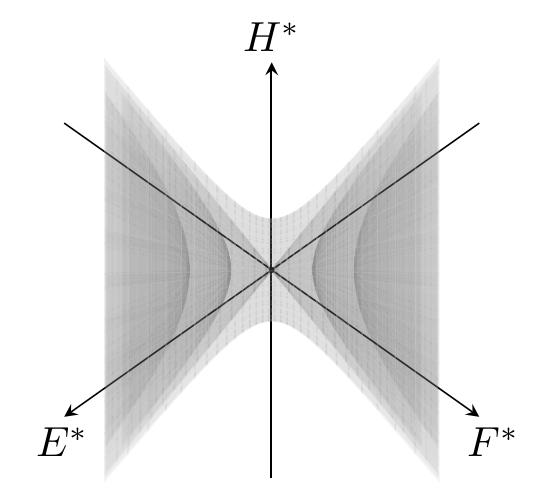
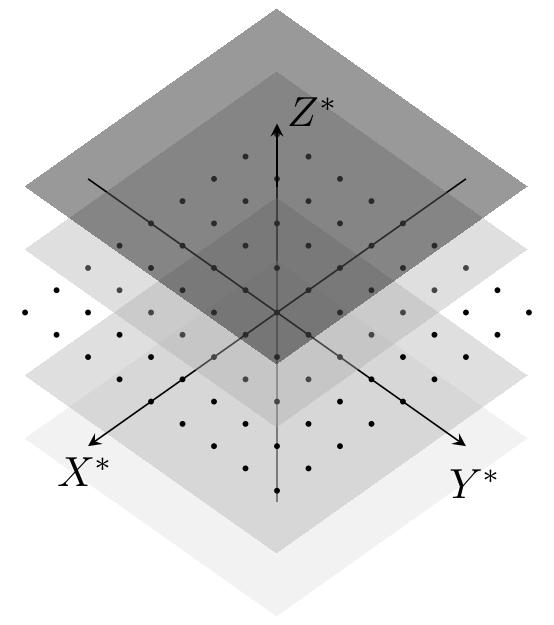
Another geometry arising from the study of Poisson structures is that of Lie algebroids and Lie groupoids, which are also a major focus of our group’s research. These follow the from the process of ‘oidification’, i.e. the transformation of certain structures into categories (in this case making a category with Lie algebra/group properties). One can show that every Poisson manifold \((M,\pi)\) has an associated Lie algebroid — its cotangent bundle \(T^\ast M\) — and, to every Lie algebroid, one can associate a Poisson structure, generalising the similar construction for Lie algebras. The global counterpart to Lie algebroids \(A\to M\) are Lie groupoids, usually denoted by \(\mathcal{G}\rightrightarrows M\). These can be shown to always give a Lie algebroid (in a similar construction of the Lie algebra of a Lie group), however, unlike the group/algebra case, it has been shown by Crainic and Fernandes, that not every Lie algebroid is integrable into a Lie groupoid. Returning to the Poisson case, whenever the Lie algebroid associated to this Poisson structure is integrable to a groupoid, one can show that the associated Lie groupoid gains a symplectic-like structure, yielding a so-called symplectic groupoid.
Understanding of all these structures (and many more) requires a plethora of different methods. First of all, differential geometry is the basis of all our work. However, understanding many of the local problems that arise in these structures requires a deep knowledge of techniques from Homological Algebra, Deformation Theory as well as several different aspects of Analysis and Topology.