2. Welche der folgenden Vektoren sind Potentiale des gegebenen Graphen?
(Mehrere Antworten sind möglich)
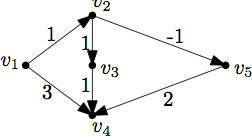
3. Welche der folgenden Graphen sind bipartit? (Mehrere Antworten sind möglich)

4. Welcher der folgenden Sätze gibt korrekt die Aussage des Matchingtheorems von König wieder? (Mehrere Antworten sind möglich)
5. Welcher $M$-augmentierende Weg wird in der ungarischen Methode zur Berechnung eines Matchings mit maximalem Gewicht im folgenden Graphen mit gegebenem Matching (fett gedruckte Kante) gewählt? (Mehrere Auswahlen sind möglich)
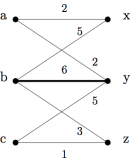
6. Seien $D=(V,A)$, $s, t \in V$ und $f$ ein $s$-$t$-Fluss. Wie sind die Kanten des Residualgraphs $D_f$ definiert? (Mehrere Auswahlen sind möglich)
7. Gegeben ist der folgende Graph mit angegebener Kapazität und maximalem s-t-Fluss (in Klammern). Für welche Mengen $U \subseteq V$ ist $\delta^{out}(U)$ ein minimaler s-t-Schnitt? (Mehrere Antworten sind möglich)
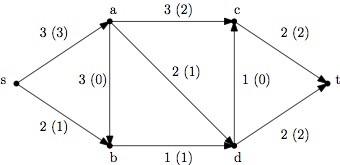
8. Welche der folgenden Mengen sind konvex?
(a) $\Big\{x\in\mathbb{R}^2 : \begin{pmatrix}1&1\\0&0\end{pmatrix}x=\begin{pmatrix}5\\1\end{pmatrix}\Big\}$
(b) $B(0,1) \setminus \{e_1\} \subseteq \mathbb{R}^n$
(c) $B(0,1) \setminus \{0\}\subseteq \mathbb{R}^n$
(d) $\operatorname{conv}\{1,2,3\}\subseteq \mathbb{R}$
(e) $\{(x,y)\in \mathbb{R}^2 : y\geq x^3\}$
9. Seien $x_1,\ldots,x_N\in\mathbb{R}^n$ und sei $y=\sum_{i=1}^N \alpha_i x_i$. Unter welchen der folgenden Bedingungen ist $y$ eine Konvexkombination der $x_i$?
(a) $\sum_{i=1}^N\alpha_i=1$ und $\alpha_i\geq 0$ für alle $i=1,\ldots,N$
(b) $\sum_{i=1}^N\alpha_i=1$
(c) $\alpha_i\geq 0$ für alle $i=1,\ldots,N$
(d) $\alpha_i\in [0,1]$ für alle $i=1,\ldots,N$
(e) $\alpha_i = 1/N$ für alle $i=1,\ldots,N$
(f) $\binom{1}{y}=\binom{1 \cdots 1}{x_1 \cdots x_N}\alpha$ mit $\alpha=(\alpha_1,\ldots,\alpha_N)^T\geq 0$
(g) $\alpha_i= 0$ für alle $i=1,\ldots,N$
10. Welche der folgenden Aussagen sind wahr?
(a) Sei $C\subseteq \mathbb{R}^n$ konvex und abgeschlossen, und sei $z\not\in C$. Dann gibt es eine Trennhyperebene von $\{z\}$ und $C$.
(b) Sei $C\subseteq \mathbb{R}^n$ konvex, und sei $z\not\in C$. Dann gibt es eine Trennhyperebene von $\{z\}$ und $C$.
(c) Falls $A$ und $B$ konvexe und abgeschlossene Mengen sind, mit $A\cap B=\emptyset$, dann gibt es eine Trennhyperebene von $A$ und $B$.
(d) Falls $A$ und $B$ konvexe und abgeschlossene Mengen sind, mit $A\cap B=\emptyset$, dann gibt es eine strikte Trennhyperebene von $A$ und $B$.
11. Für welche der folgenden Mengen $P$ gilt $P=\operatorname{conv}(\operatorname{ext}(P))$?
12. Wieviele Ecken hat das Polyeder $P=\{x\in\mathbb{R}^3 : Ax\leq b\}$, wobei
$$ A=\begin{pmatrix} -1&0&0\\0&-1&0\\0&0&-1\\1&0&0\end{pmatrix},b=\begin{pmatrix}0\\0\\0\\5\end{pmatrix}$$
13. Seien $A\in\mathbb{R}^{m\times n}$ und $b\in\mathbb{R}^m$ gegeben.
Welche der folgenden Aussagen sind wahr?
(a) Es gibt einen Vektor $x\in\mathbb{R}^n$ mit $x\geq 0$ und $Ax=b$ genau dann, wenn es keinen Vektor $y\in\mathbb{R}^m$ gibt, der $A^Ty\geq 0$ und $b^Ty<0$ erfüllt.
(b) Es gibt einen Vektor $x\in\mathbb{R}^n$ mit $Ax\leq b$ genau dann, wenn es keinen Vektor $y\in\mathbb{R}^m$ gibt, der $y\geq 0$, $A^Ty= 0$ und $b^Ty= 2017$ erfüllt.
(c) Es gibt einen Vektor $x\in\mathbb{R}^n$ mit $Ax\leq b$ genau dann, wenn es keinen Vektor $y\in\mathbb{R}^m$ gibt, der $y\geq 0$, $A^Ty= 0$ und $b^Ty= -2017$ erfüllt.
14. Seien $c\in\mathbb{R}^n$, $A\in\mathbb{R}^{m\times n}$ und $b\in\mathbb{R}^m$ gegeben. Sei
$$p^*=\sup\{c^Tx : x\in\mathbb{R}^n, Ax\leq b\}$$
und
$$d^*=\inf\{b^Ty : y\in\mathbb{R}^m, y\geq 0, A^Ty=c\}.$$
Welche der folgenden Aussagen ist wahr?
(a) $p^*\leq d^*$.
(b) $p^*\geq d^*$.
(c) Falls es für beide Programme zulässige Vektoren gibt, dann ist $p^*=d^*$.
(d) Falls es für beide Programme zulässige Vektoren gibt, dann ist $p^* \geq d^*$.
(e) Es ist $p^*=-\infty$, falls es keine zulässigen Vektoren für das obige Maximierungsprogramm gibt.
15. Mit dem Verfahren von Fourier und Motzkin kann man:
16. Welche der folgenden Aussagen sind wahr?
17. Sei $G$ ein ungerichteter bipartiter Graph und $A$ seine Inzidenzmatrix. Welche der folgenden Programme berechnen die Matchingzahl von $G$?
(a) $\max\{1^Tx : x\in\mathbb{R}^E_{\geq 0}, Ax\leq 1\}$.
(b) $\min\{1^Ty : y\in\mathbb{Z}^V_{\geq 0}, A^Ty\geq 1\}$.
(c) $\max\{1^Tx : x\in\mathbb{Z}^E_{\geq 0}, Ax\geq 1\}$.
(d) $\min\{1^Ty : y\in\mathbb{R}^V_{\geq 0}, A^Ty\leq 1\}$.