 |

Fucik Spectrum of the Laplace Operator
A simplified model of a suspension bridge [4] can
serve as an example of an application related to the
Fucik spectrum. The model involves the term 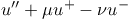 , where , where 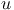 stands for the (vertical) deflection of the roadbed
at a certain point of the bridge,
stands for the (vertical) deflection of the roadbed
at a certain point of the bridge, 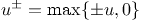 ,
and the two coefficients (spring constants) ,
and the two coefficients (spring constants) 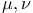 describe different forces applied
by the cables when they are tight describe different forces applied
by the cables when they are tight 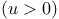 or
slack or
slack 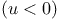 . (Here is
more on another model of a suspension bridge.) . (Here is
more on another model of a suspension bridge.)
The Fucik spectrum of the Laplace operator is the
set of all pairs 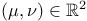 for
which the following problem has a nontrivial
solution for
which the following problem has a nontrivial
solution 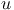 in the Sobolev space in the Sobolev space 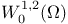 : :
where 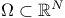 is a
bounded domain. is a
bounded domain.
In the late 70's it was discovered by S. Fucik
[2] and E. N. Dancer [1] that the existence of
solutions of the nonlinear problem
with 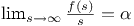 , , 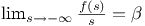 depends on the position of the pair
of numbers depends on the position of the pair
of numbers 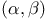 in the real plane in the real plane 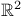 with
respect to the "curves" of the Fucik spectrum. with
respect to the "curves" of the Fucik spectrum.
Together with Wolfgang Reichel we took a look at
this problem in [3]. We studied it using both a
variational formulation and an implicit function
argument. In addition to analytical results we also
performed numerical computations on several domains
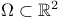 in the plane. The two figures show
some of these computations. Figure 1 shows a part of
the Fucik spectrum computed for a triangular domain
(one should note the bifurcation of the curves and
their crossing), Figure 2 shows one Fucik
eigenfunction in the plane. The two figures show
some of these computations. Figure 1 shows a part of
the Fucik spectrum computed for a triangular domain
(one should note the bifurcation of the curves and
their crossing), Figure 2 shows one Fucik
eigenfunction 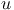 on
this domain. on
this domain.
References
| [1] |
E. N. Dancer, On the
Dirichlet problem for weakly nonlinear elliptic
partial differential equations,
Proc. Roy. Soc. Edinburgh Sect. A 76 (1997)
283-300. |
| [2] |
S. Fucik, Solvability of
nonlinear equations and boundary value problems,
Mathematics and its applications, Vol. 4, Reidel,
Dordrecht/Boston, 1980. |
| [3] |
J. Horak, W. Reichel,
Analytical and numerical results for the Fucik
spectrum of the Laplacian,
J. Comput. Appl. Math. 161 (2003) 313-338. |
| [4] |
A.C. Lazer, P. J. McKenna,
Existence, uniqueness, and stability of
oscillations in differential equations with
asymmetric nonlinearities,
Trans. Amer. Math. Soc. 315 (1989) 721-739. |
 |
 |
|
|
 |

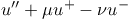 , where
, where 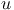 stands for the (vertical) deflection of the roadbed
at a certain point of the bridge,
stands for the (vertical) deflection of the roadbed
at a certain point of the bridge, 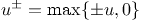 ,
and the two coefficients (spring constants)
,
and the two coefficients (spring constants) 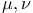 describe different forces applied
by the cables when they are tight
describe different forces applied
by the cables when they are tight 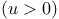 or
slack
or
slack 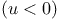 . (
. (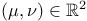 for
which the following problem has a nontrivial
solution
for
which the following problem has a nontrivial
solution 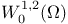 :
: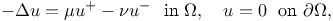
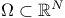 is a
bounded domain.
is a
bounded domain.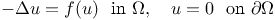
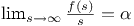 ,
, 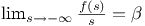 depends on the position of the pair
of numbers
depends on the position of the pair
of numbers 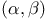 in the real plane
in the real plane 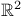 with
respect to the "curves" of the Fucik spectrum.
with
respect to the "curves" of the Fucik spectrum.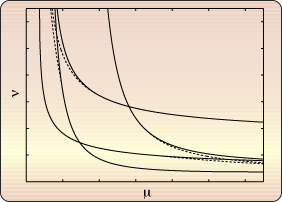
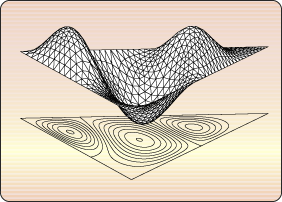
 in the plane. The two figures show
some of these computations. Figure 1 shows a part of
the Fucik spectrum computed for a triangular domain
(one should note the bifurcation of the curves and
their crossing), Figure 2 shows one Fucik
eigenfunction
in the plane. The two figures show
some of these computations. Figure 1 shows a part of
the Fucik spectrum computed for a triangular domain
(one should note the bifurcation of the curves and
their crossing), Figure 2 shows one Fucik
eigenfunction