Snapshot: Purely hyperbolic gravity simulations with Trixi.jl

One of the challenges when simulating astrophysical flows with self-gravity is to compute the gravitational forces. In contrast to the hyperbolic compressible Euler equations, the gravity field is described by an elliptic Poisson equation. In [1], we present a purely hyperbolic approach by reformulating the elliptic problem into a hyperbolic diffusion problem, which is solved in pseudotime using the same explicit high-order discontinuous Galerkin method we use for the flow solution.

We start with the Poisson equation for the Newtonian gravitational potential $\phi$,

$$-\vec{\nabla}^2\phi = -4\pi G \rho\label{grav}$$

where G is the universal gravitational constant and $\rho$ is the mass density. Following Nishikawa’s work, we convert the Poisson equation for the gravitational potential into the hyperbolic gravity equations,

$$\frac{\partial}{\partial t}\begin{bmatrix}
\phi\\[0.1cm]
q_1\\[0.1cm]
q_2\\[0.1cm]
\end{bmatrix}
+
\frac{\partial}{\partial x}\begin{bmatrix}
-q_1\\[0.1cm]
-\phi/T_r\\[0.1cm]
0\\[0.1cm]
\end{bmatrix}
+
\frac{\partial}{\partial y}\begin{bmatrix}
-q_2\\[0.1cm]
0\\[0.1cm]
-\phi/T_r\\[0.1cm]
\end{bmatrix}
=
\begin{bmatrix}
-4\pi G \rho\\[0.1cm]
-q_1/T_r\\[0.1cm]
-q_2/T_r\\[0.1cm]
\end{bmatrix},\label{hyp}$$

where the auxiliary variables $(q_1,q_2)^\intercal\approx\vec{\nabla}\phi$ and $T_r$ is the relaxation time. The steady-state solution of the hyperbolic system is, in fact, the desired solution of the original Poisson problem.

The flow and the gravity solvers operate on a joint hierarchical Cartesian mesh and are two-way coupled in each Runge-Kutta stage via the source terms. A key benefit of our strategy is that it allows the reuse of existing explicit hyperbolic solvers without modifications, while retaining their advanced features such as non-conforming and solution-adaptive grids.

We implemented this purely hyperbolic approach for self-gravitating gas dynamics in Trixi.jl, a tree-based numerical simulation framework for hyperbolic PDEs, which is written in Julia [2]. It was first validated by computing the Jeans gravitational instability, which demonstrates excellent agreement of the numerical results with the analytical solution:

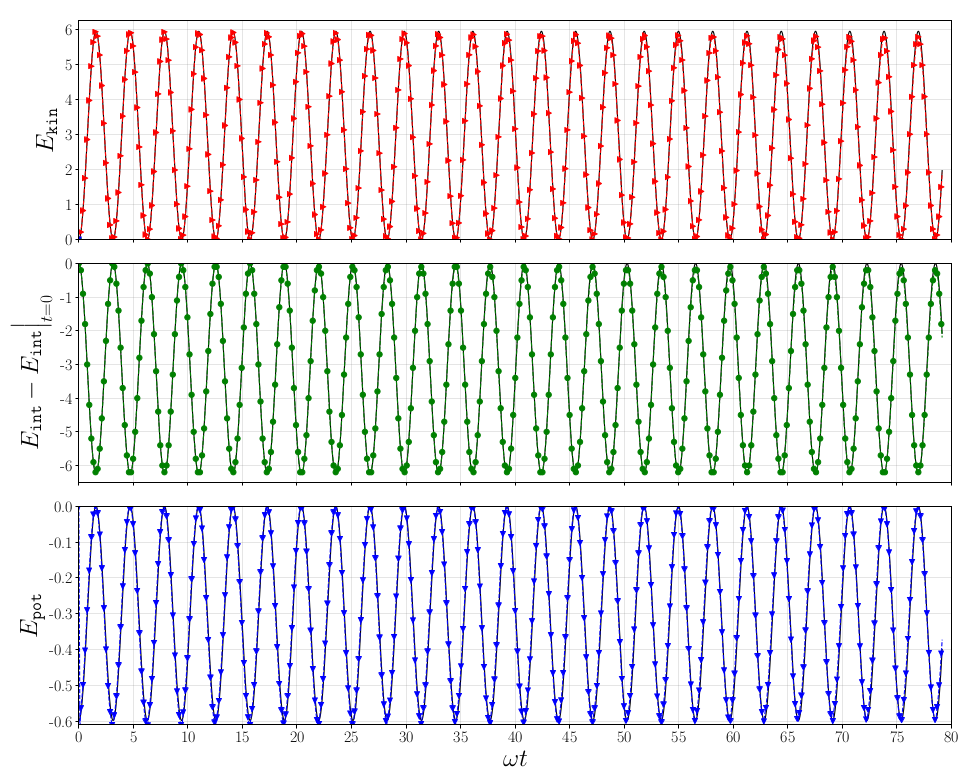
Evolution of the computed kinetic, internal, and potential energies for the Jeans
instability using polynomial order N = 3 on a uniform 16 × 16 mesh. The analytical energies are included for reference.

In a second example, we consider a modification of the Sedov blast wave problem that incorporates the effects of gravitational acceleration and which involves strong shocks and complex fluid interactions. We include it to demonstrate the shock capturing and AMR capabilities of Trixi.jl to resolve the cylindrical Sedov blast wave:

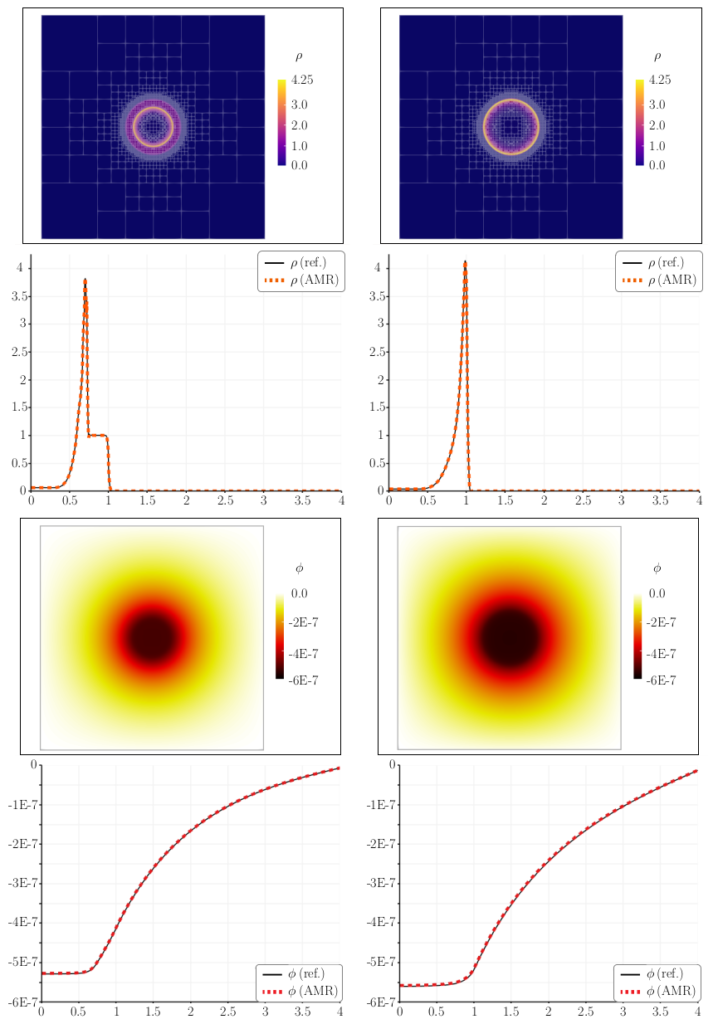
Self-gravitating Sedov explosion approximated with polynomial order $N = 3$ on an AMR grid with four levels of possible refinement at $T = 0.5$ (left) and $T = 1.0$ (right). (first and third row) Two dimensional plots of the density and gravitational potential at two times. The white overlay of squares in the density plots shows the AMR grids used by both solvers. (second and last row) One dimensional slices of the solutions along a line from the origin to the edge of the domain in the positive x-direction.

Finally, we show the evolution of the solution together with the adaptive mesh, which is dynamically refined and coarsened to maintain high accuracy while reducing the overall computation time:

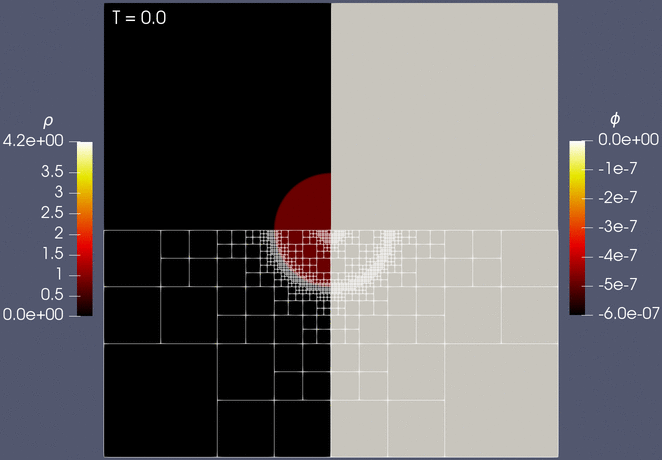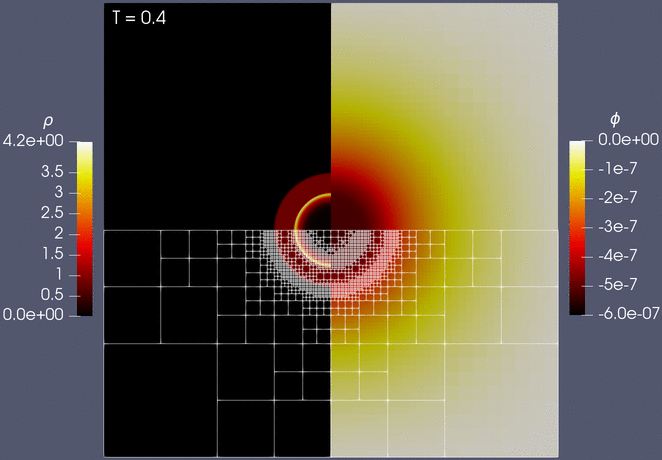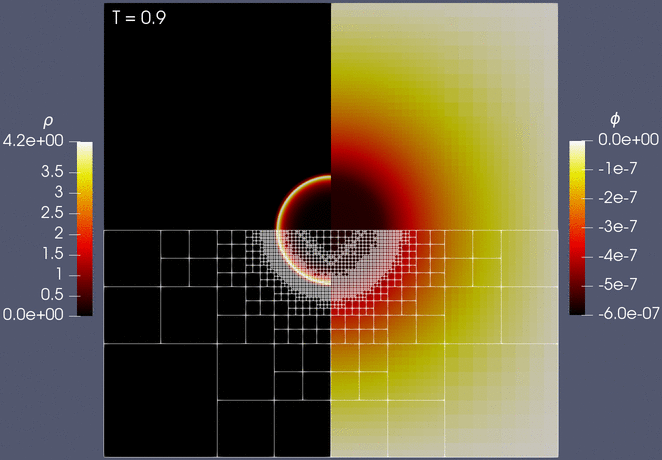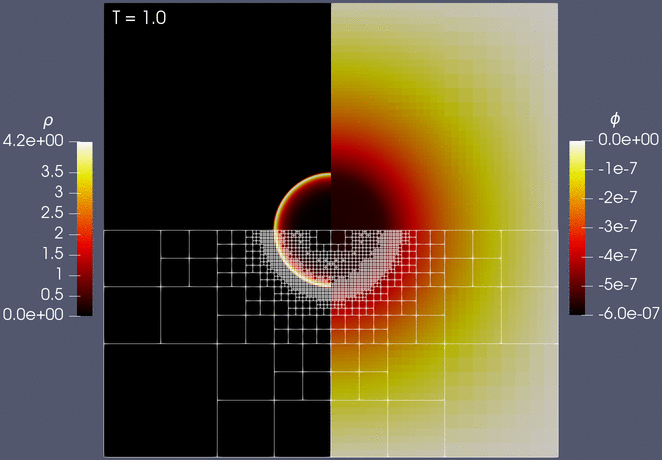
https://raw.githubusercontent.com/trixi-framework/paper-self-gravitating-gas-dynamics/master/assets/sedov-rho-phi-mesh.gif
Simulation of self-gravitating Sedov blast wave with adaptive mesh refinement, where adaptation performed after every time step of the compressible Euler solver. The total run time compared to a uniformly refined mesh is reduced by a factor of 19, while the solutions are virtually unchanged.

All results in the paper can be easily reproduced by using the resources provided in [3], including step-by-step instructions for how to obtain and install Trixi.jl.

References

[1] Schlottke-Lakemper, Michael and Winters, Andrew R and Ranocha, Hendrik and Gassner, Gregor J, A purely hyperbolic discontinuous Galerkin approach for self-gravitating gas dynamics, submitted to J Comp Phys, 2020. arXiv:2008.10593

[2] Schlottke-Lakemper, Michael and Gassner, Gregor J and Ranocha, Hendrik and Winters, Andrew R, Trixi.jl: A tree-based numerical simulation framework for hyperbolic PDEs written in Julia, 2020. doi:10.5281/zenodo.3996439

[3] Schlottke-Lakemper, Michael and Winters, Andrew R and Ranocha, Hendrik and Gassner, Gregor J, Self-gravitating gas dynamics simulations with Trixi.jl, 2020. doi:10.5281/zenodo.3996575