- Snapshot: Barotropic Instability with and without Orography February 10, 2025
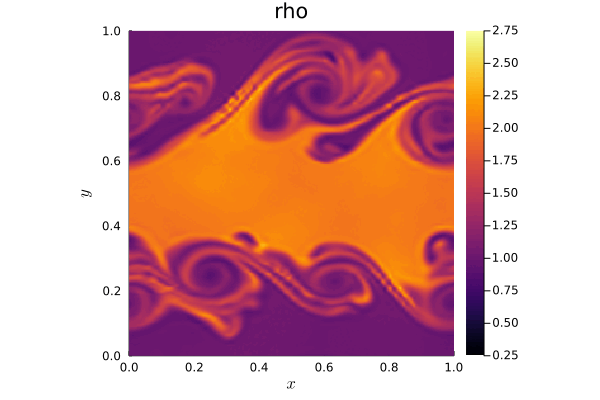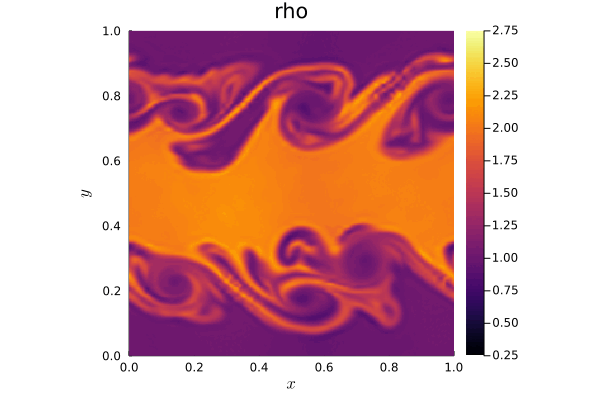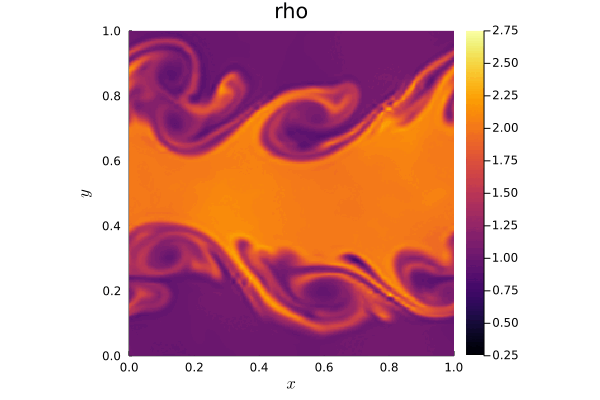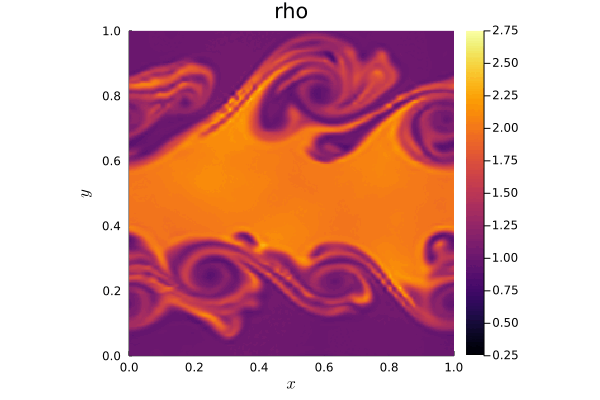
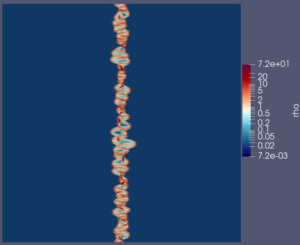
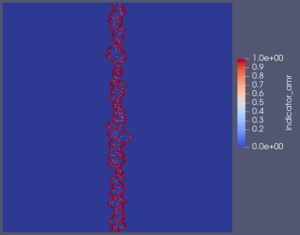
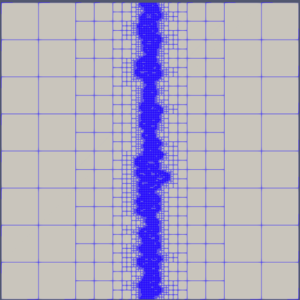
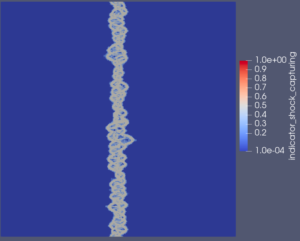
The video shows the evolution of a barotropic instability in Earth’s polar jet stream. Initially uniform, the jet stream undergoes perturbations, leading to vortex formation driven by the Coriolis force due to Earth’s rotation. To simulate this phenomenon, we discretize the Shallow Water Equations on the sphere using a discontinuous Galerkin method. We compare two scenarios: an ocean-covered Earth (without orography) and a more realistic representation that includes Earth’s orography. Orography is incorporated into the equations as a non-conservative term, with values sourced from the ETOPO dataset provided by the National Oceanic and Atmospheric Administration (NOAA). The simulations are performed using TrixiAtmo.jl.
- New paper published: TrixiParticles.jl: Particle-based multiphysics simulation in Julia January 28, 2025
Our new paper “TrixiParticles.jl: Particle-based multiphysics simulation in Julia” has been published in the Journal of Open Source Software.
We are happy we were able to contribute to the publication and thank all our collaborators for the great experience.Summary
TrixiParticles.jl is a Julia-based open-source package for particle-based multiphysics simulations and part of the Trixi Framework. It handles complex geometries and specialized applications, such as computational fluid dynamics (CFD) and structural dynamics, by providing a versatile platform for particle-based methods. TrixiParticles.jl allows for the straightforward addition of new particle systems and their interactions, facilitating the setup of coupled multiphysics simulations such as fluid-structure interaction (FSI). Furthermore, simulations are set up directly with Julia code, simplifying the integration of custom functionalities and promoting rapid prototyping
- Snapshot: Hyperbolic viscous flow – Three-dimensional cubic Lid-Driven Cavity December 20, 2024
This research has been carried out by Simone Chiocchetti, funded by the European Union’s Horizon Europe Research and Innovation Programme under the Marie Skłodowska-Curie Postdoctoral Fellowship MoMeNTUM (grant agreement No. 101109532).
x-z central cross section of 3d Lid-Driven Cavity flow, solving the unified model of Godunov, Peshkov, and Romenski for hyperbolic viscous flow. The upper row shows the macroscopic flow state, while the bottom row shows the distortion field, tracking fluid flow deformations as if it were a solid. The numerical solver is a simple explicit second order Finite Volume method (MUSCL-Hancock) using an HLL-type Riemann solver based on Toro-Vazquez flux splitting. The Reynolds number is 1000 and the mesh resolution is 384^3.
- Snapshot: Postdoctoral researcher Dr. Boqiang Huang joins our research group November 7, 2024
Boqiang Huang received his Ph.D. in Biomedical Engineering from the Department of Electronic Engineering at Fudan University, Shanghai, China, in 2010. Following his doctoral studies, he was awarded the Alexander von Humboldt Postdoctoral Fellowship and worked under the mentorship of Prof. Angela Kunoth. During this time, he contributed as a research scientist in Prof. Kunoth’s group (AG-Kunoth) at the Institute of Mathematics, University of Paderborn, and later at the University of Cologne. In 2021, Dr. Huang joined the group of Prof. Dorit Merhof (AG-Merhof) at the Institute of Imaging and Computer Vision at RWTH Aachen University, and subsequently at the University of Regensburg. His research expertise spans multiple disciplines in the field of data science, including biomedical engineering, electronic engineering, applied mathematics and applied physics.
In July 2024, Dr. Huang became a research scientist in the group of Prof. Gregor Gassner (AG-Gassner). He is also supported by the HESCOR research project (“Human & Earth System Coupled Research” https://hescor.uni-koeln.de/). His current research focuses on the “Machine learning & Culture Clusters” over large timescales, ranging from the Paleolithic era (1.4 million to 24,000 years ago) to the present. He collaborates with researchers from archaeology, geophysics, and the humanities on this interdisciplinary project.
- Snapshot: Postdoctoral researcher Dr. Tristan Montoya joins our research group August 28, 2024

Tristan Montoya completed his PhD at the University of Toronto Institute for Aerospace Studies under the supervision of Prof. David W. Zingg. His doctoral work focused on the development and analysis of provably stable discontinuous spectral-element methods (DSEMs) with the summation-by-parts property for systems of conservation laws, particularly on triangular and tetrahedral meshes.Tristan joined the Numerical Simulation research group at the University of Cologne in January 2024, and is part of the Trixi.jl development team. His current research involves the development of split-form and entropy-stable DSEMs for atmospheric models and their application to global weather and climate prediction. You can keep up-to-date with Tristan’s research and software contributions on his Google Scholar and GitHub pages, as well as on his personal website.
- Snapshot: Multiphysics SPH simulation of the liquefaction of the Julia logo July 4, 2024
2D single-phase simulation of the liquefaction of the Julia logo with TrixiParticles.jl. The letters are simulated as a fluid with the Weakly Compressible SPH (WCSPH) method and the dots are simulated as an elastic solid with the Total Lagrangian SPH (TLSPH) method for structure mechanics.
This Snapshot was created by Niklas Neher (https://www.hlrs.de/de/team/niklas-neher).
- Snapshot: Discontinuous Galerkin Solver for the Spherical Shallow Water Equations May 31, 2024
A preliminary step in the development of a global atmospheric model is the construction of a suitable horizontal discretization for partial differential equations in spherical geometry. The spherical shallow water equations, which consist of a scalar equation governing mass conservation coupled with a vector equation for the momentum balance under gravitational and Coriolis forces, serve as a simplified model for the horizontal dynamics of the Earth’s atmopheric circulation. Since the spherical shallow water equations exhibit many of the characteristic features and numerical challenges associated with atmospheric fluid flow, they provide a useful testbed for the development and assessment of numerical schemes for weather prediction and climate modelling (see, for example, Williamson et al. [1]).
By extending Trixi.jl to solve hyperbolic partial differential equations on curved manifolds, we are able to simulate shallow-water flows on the surface of the sphere using discontinuous Galerkin methods formulated with respect to the two-dimensional tangent space associated with a cubed-sphere grid [2, 3]. The video below depicts the relative vorticity field for the numerical solution to the spherical shallow water equations in flux form, which we discretize similarly to Bao et al. [4] using a discontinuous Galerkin method employing 5400 curved quadrilateral elements of polynomial degree seven. The initial condition corresponds to a mid-latitude jet with a small perturbation added to initiate a barotropic instability, which was proposed by Galewsky et al. [5] as a test case exhibiting complex nonlinear dynamics characteristic of those present in numerical weather prediction and climate models.
References[1] D. L. Williamson, J. B. Drake, J. J. Hack, R. Jakob, and P. N. Swarztrauber. A standard test set for numerical approximations to the shallow water equations in spherical geometry. Journal of Computational Physics, 102(1):211-224, 1992.
[2] R. Sadourny. Conservative finite-difference approximations of the primitive equations on quasi-uniform spherical grids. Monthly Weather Review, 100(2):136-144, 1972.
[3] C. Ronchi, R. Iacono, and P. S. Paolucci. The “cubed sphere”: A new method for the solution of partial differential equations in spherical geometry. Journal of Computational Physics, 124(1):93-114, 1996.
[4] L. Bao, R. D. Nair, and H. M. Tufo. A mass and momentum flux-form high-order discontinuous Galerkin shallow water model on the cubed-sphere. Journal of Computational Physics, 271:224-243, 2014.
[5] J. Galewsky, R. K. Scott, and L. M. Polvani. An initial-value problem for testing numerical models of the global shallow-water equations. Tellus A, 56(5):429–440, 2004.
This snapshot was created by Tristan Montoya.
- Snapshot: Postdoctoral researcher Dr. Simone Chiocchetti joins our research group April 11, 2024

Simone Chiocchetti studied Civil, Environmental, and Mechanical Engineering at the University of Trento, Italy, under the supervision of Prof. Dr.-Ing. Michael Dumbser.
He spent a year in Stuttgart at the IAG (Institute of Aerodynamics and Gasdynamics), funded by the DFG project “DROPIT startup grant” and he is currently working at the University of Cologne in the Numerical Simulation Research group led by Prof. Dr.-Ing. Gregor Gassner, under a Marie Skłodowska-Curie Postdoctoral Fellowship (European Union’s Horizon Europe Research and Innovation Programme, grant agreement No. 101109532).
Simone’s research interests include: high order numerical methods, of the Finite Volume and Discontinuous Galerkin families, in the context of first order hyperbolic partial differential equations; algorithms for generation and optimization of high quality unstructured meshes; treatment of stiff algebraic source terms; modeling of fluid and solid mechanics as well as multiphase flow; high-performance computing; semi-implicit numerical methods.
Simone’s current MSCA project (MoMeNTUM: Modern high order numerical Methods based on No-compromise moving Voronoi Tessellations, a Unified solver for continuum Mechanics) concerns the development of high order numerical methods on Voronoi grids, together with new meshing algorithms that allow to fully take advantage of the versatility provided by unstructured moving polygonal meshes, with special attention to the computational efficiency of the implementation.
- Snapshot: Postdoctoral researcher Dr. Aleksey Sikstel joins our research group March 28, 2024

Aleksey defended his doctoral thesis on coupling of hyperbolic conservation laws in 2020 at the RWTH Aachen University while working with Prof. Siegfried Müller and Prof. Michael Herty. After that he continued working with Prof. Jan Giesselmann at the TU Darmstadt on a posteriori error estimators for systems of hyperbolic conservation laws before switching to Cologne in 2022.Alekseys research focus lies on adaptivity for high-order numerical methods for hyperbolic conservation laws, coupling of conservation laws via sharp interfaces, multiphase flows and stochastic-Galerkin PDE. In the Numerical Simulation Research Group Aleksey is working on multi-ion MHD systems and novel coupling and temporal schemes within the Snubic-project.
- Snapshot: Postdoctoral researcher Dr. Benedict Geihe joins our research group February 21, 2024

Benedict Geihe studied Mathematics and Computer Science at the University of Bonn, Germany. After graduation he joined the research group of Professor Martin Rumpf at the Institute for Numerical Simulation as a research and teaching assistant. In his PhD studies he investigated and implemented finite element based numerical simulation and shape optimization of multi-scale microstructures in elastic composite materials.
Benedict then moved to the German Aerospace Center (DLR) and worked as a researcher at the Numerical Methods department of the Institute of Propulsion Technology. He was part of the development team of the flow solver TRACE, used for academic and industrial simulation and analysis of flows in turbomachines. His research covered resonance phenomena induced by fluid structure interaction and frequency based numerical methods.
Benedict is now part of the Numerical Simulation Research Group at the University of Cologne, where he joined the Trixi.jl development team. He is currently working on project ADAPTEX, funded by the German Federal Ministry of Education and Research within the SCALEXA initiative. The objective is to deploy Trixi.jl in exascale-capable flow simulations on CPUs and GPUs for applications in earth system modeling on dynamic adaptive meshes.
- Snapshot: 2D Sloshing simulation January 26, 2024
2D Sloshing simulation in a round tank oscillating from left to right. The simulation was done with the CFD code Trixi.jl [1] which was extended with a three-equations model [2]. The model consists of a two-phase flow simplification of the Baer–Nunziato equations of compressible multi-phase flows [3]. The shown simulation is part of combined research efforts of the German Aerospace Center (DLR) and the University of Cologne to create computational models of sloshing dynamics in liquid hydrogen storage systems on mobile platforms such as cars, ships, and planes.
References:
[1] https://trixi-framework.github.io/
[2] Dumbser, Michael. “A simple two-phase method for the simulation of complex free surface flows.” Computer methods in applied mechanics and engineering 200.9-12 (2011): 1204-1219.
[3] M.R. Baer, J.W. Nunziato: “A two-phase mixture theory for the deflagration-todetonation transition (DDT) in reactive granular materials”, J. Multiphase Flow 12 (1986) 861–889.
[4] Project HyTaZer: https://elib.dlr.de/201347/ and https://www.dlr.de/sy/PortalData/17/Resources/dokumente/wissenschaftstag/2022/6_Wissenschaftstag_2022_Hytazer_Freund.pdfThis Snapshot was created by Johannes Markert (http://jmark.de/).
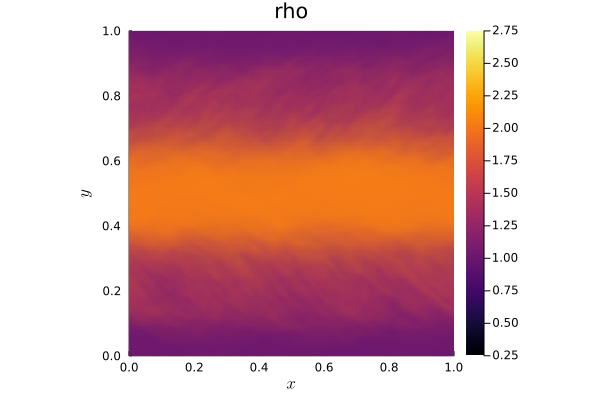
- Snapshot: Discontinuous Galerkin simulation on a spherical shell December 1, 2023
Utilizing a mapping $(\xi, \eta) \in \mathbb{R}^2 \rightarrow (x, y, z) \in \mathbb{R}^3$ and specifically tailored tensor-product Legendre–Gauss–Lobatto basis functions [1,2], discontinuous Galerkin (DG) simulations can be performed on a curved surface. In particular, we are interested in running DG simulations on a spherical shell.
To achieve this, we create a two-dimensional cubed-sphere mesh for tessellating the sphere’s surface. This mesh proves advantageous as it avoids singularities at the poles present in latitude-longitude grids, while still facilitating a highly regular tessellation of the simulation domain through the use of quadrilaterals.
Within this mesh, we address the linear advection equations incorporating position-dependent advection velocity:
\[ \frac{\partial \rho}{\partial t} + \nabla \cdot \left( \vec{v} (x, y, z) \rho \right) = 0. \]
Additionally, a solid-body rotation velocity tangential to the spherical surface is imposed.The presented video showcases the advection of a Gaussian pulse across the globe using Trixi.jl (https://github.com/trixi-framework/Trixi.jl) with the two-dimensional p4est solver. The simulation also incorporates a custom implementation of the three-dimensional linear advection equations.
References[1] Song, C. & Wolf, J. P. (1999). The scaled boundary finite element method—alias consistent infinitesimal finite element cell method—for diffusion. International Journal for Numerical Methods in Engineering, 45(10), 1403-1431.
[2] Giraldo, F. X. (2001). A spectral element shallow water model on spherical geodesic grids. International Journal for Numerical Methods in Fluids, 35(8), 869-901. - Snapshot: Blending Finite Volume Fluxes with Reinforcement Learning October 27, 2023
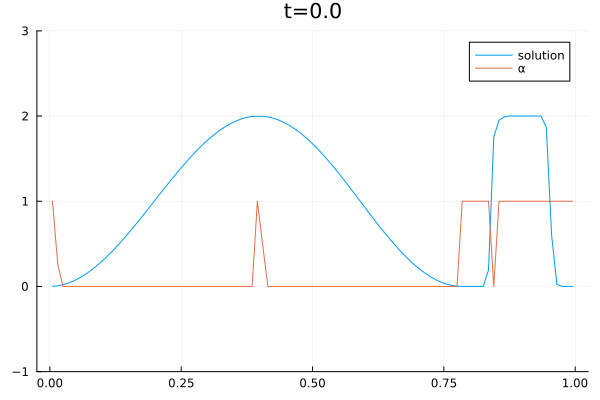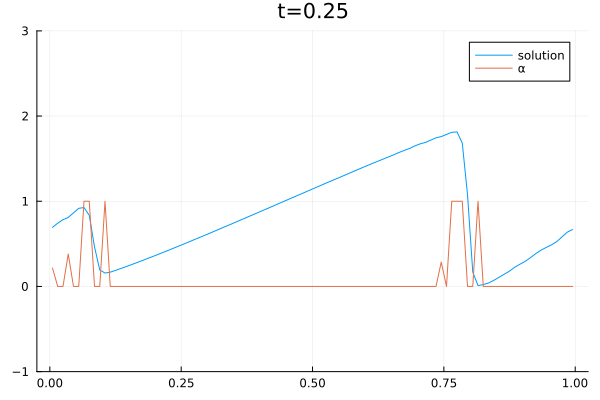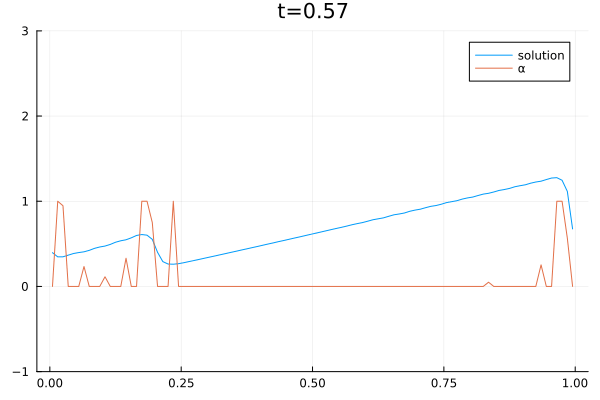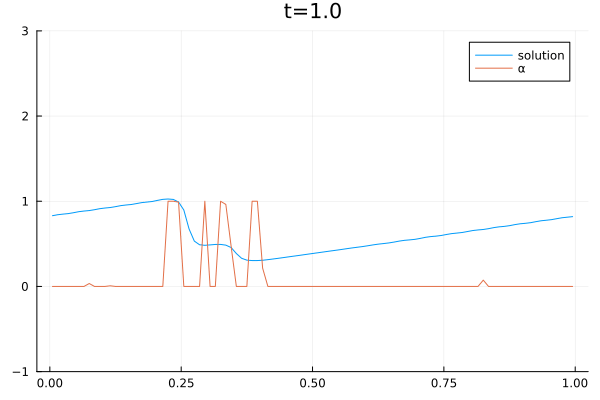
When solving PDEs with the finite volume method, one must choose a numerical flux function. We use a convex combination of the central flux $F^C$ and local Lax Friedrich flux $F^{LLF}$ to solve the Burgers equation.
\begin{align*}
&u_t + \left(\frac{u^2}{2}\right)_x =0\\
&\frac{du_j}{dt} =\frac{1}{\Delta x} \left[ \alpha_j \left(F_{j-1/2}^{LLF} -F_{j+1/2}^{LLF}\right) + (1-\alpha_j)\left(F_{j-1/2}^{C} – F_{j+1/2}^{C}\right) \right]
\end{align*}The central flux is highly accurate but can lead to oscillating and thus unstable solutions. The local Lax Friedrich flux is stable but also dissipative. Therefore, we want to choose alpha so that the solution is stable and at the same time as accurate as possible. We train a Reinforcement Learning Agent to choose alpha. One agent performs locally in one grid cell. The action of agent j is $\alpha_j$ and the state is given by
\begin{equation*}
r_j=\frac{u_j – u_{j-1}}{u_{j+1} – u_{j}}.
\end{equation*}The policy is a Neural Network with one hidden layer of size 10, a relu activation function in the first layer, and a hard sigmoid function in the output layer. The deep deterministic policy gradient (DDPG) approach is used to train the agent.
The video below shows the chosen amount of local Lax Friedrich flux and the resulting solution of the Burgers equation. The initial solution is a sine wave with two discontinuities. Randomly changed variants of this were used for training.
The agent performs well in unseen situations, e.g. negative sine wave, as shown below.
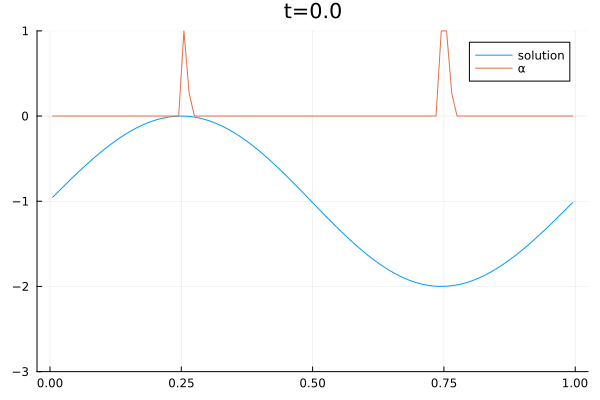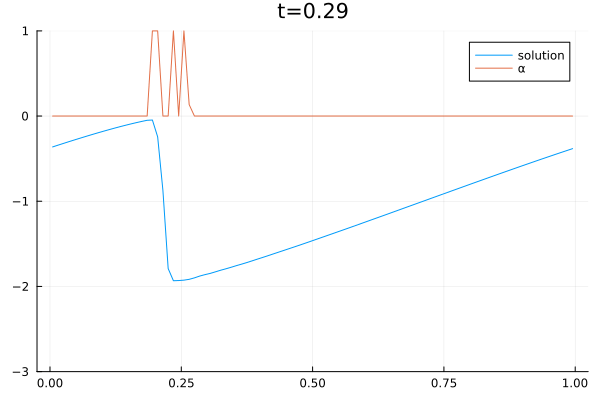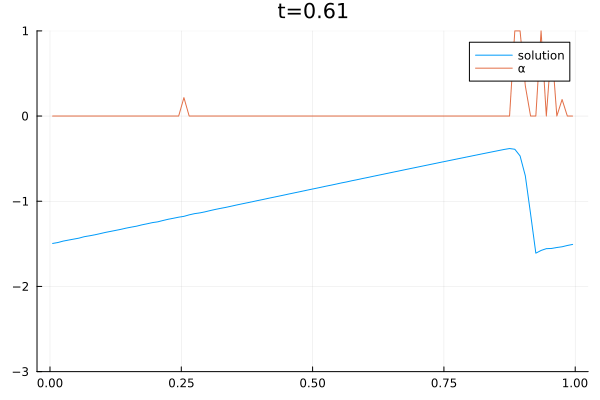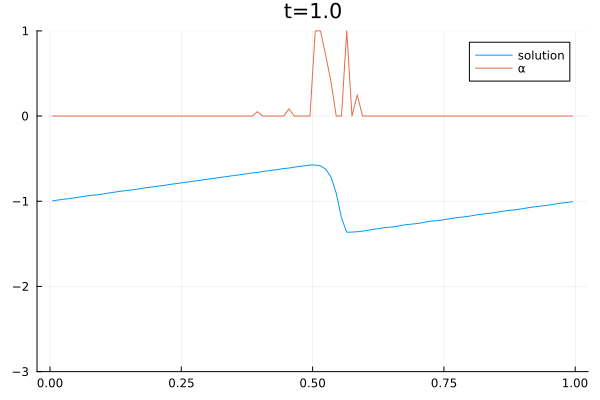
- Open Postdoctoral Positions in Scientific Computing and Machine Learning September 29, 2023
In the framework of the new project on “Cultural Evolution in Changing Climate: Human and Earth System Coupled Research (HESCOR)”, we invite applications for postdoctoral research associate positions in the area of Earth system modeling, Human system modeling, applied numerical mathematics, scientific computing and/or machine learning, among many others.
The job descriptions, duty statement and qualification requirements for each of these positions can be found on the websites:
https://imfess.uni-koeln.de/hescor/positions and
https://ufg.phil-fak.uni-koeln.de/hescorThe research associate RA6 (RA in Scientific Computing) will be hosted at the Numerical Simulation Research Group of the University of Cologne.
We provide a collaborative and friendly environment for cutting edge research and ensure measures are in place to promote early-career researchers.
- Studentische/Wissenschaftliche Hilfskraft (w/m/d) zur Betreuung und Weiterentwicklung einer automatisierten Testumgebung für den Strömungslöser Trixi gesucht September 4, 2023
In der Arbeitsgruppe von Prof. Gassner beschäftigen wir uns mit mehrskaligen Strömungsproblemen in verschiedenen physikalischen Disziplinen. Um numerisch effizient simulieren zu können, wurde in den vergangenen Jahren der Strömungslöser Trixi entwickelt, basierend auf der modernen und nutzerfreundlichen Programmiersprache Julia. Die Arbeit der zahlreichen Entwickler wird auf github koordiniert und ermöglicht automatisierte Prozesse im Rahmen von continuous integration, testing und benchmarking. Des Weiteren wurde kürzlich mit der Entwicklung einer C/Fortran-Schnittstelle begonnen, die künftig interessierten Anwender möglichst einfach zur Verfügung gestellt werden soll.
Für die Wartung und Weiterentwicklung der automatisierten Prozesse sowie der Schnittstelle suchen wir ab sofort interessierte Hilfskräfte. Technische Vorkenntnisse im Bereich des Software-Engineering unter Linux sind vorteilhaft, aber nicht zwingend nötig. Die Arbeit bietet Gelegenheit, sich in die Thematik einzuarbeiten. Der Starttermin sowie die Wochenstundenzahl können flexibel vereinbart werden. Bei Interesse wenden Sie sich gerne an bgeihe@uni-koeln.de, so dass wir Ihnen vor Ort weitere Details vorstellen können.
- Snapshot: Second-order FV method on hybrid mesh using t8code August 25, 2023
This FV simulation uses linear reconstruction to reach second order. The minmod slope limiter is used. The mesh contains triangles and quads and is a high-resolution version (with 327680 cells) of this one:
It is created and organized using t8code.
The simulation uses an initial condition with a pressure blast wave in the center and periodic boundaries.
- Snapshot: SPH Simulation of an Elastic Ball Falling Into a Tank of Water July 28, 2023
This simulation uses weakly compressible smoothed particle hydrodynamics for the fluid and a total Lagrangian SPH formulation for the elastic solid.
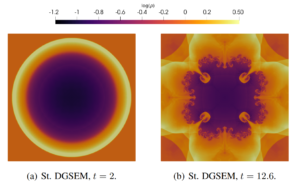
- Snapshot: Subcell limiting results for DGSEM simulations June 2, 2023
DGSEM simulations of the two-dimensional Euler equations considering the astrophysical jet with Mach number $\textrm{Ma} \approx 2000$ [1].
The computational domain, $\Omega = [-0.5,0.5]^2$, is filled with a mono-atomic gas ($\gamma = 5/3$) at rest with\begin{equation}
\rho(x,y) = 0.5, \qquad
p(x,y) = 0.4127, \qquad
v_1(x,y) = 0, \qquad
v_2(x,y) = 0,
\end{equation}and on the left boundary there is a hypersonic inflow with
\begin{equation}
\rho(-0.5,y_B) = 5, ~
p(-0.5,y_B) = 0.4127, ~
v_1(-0.5,y_B) = 800, ~
v_2(-0.5,y_B) = 0,
\end{equation}for $y_B \in [-0.05, 0.05]$, which corresponds to a Mach number of $\textrm{Ma}=2156.91$ with respect to the speed of sound of the jet gas, and $\textrm{Ma}=682.08$ with respect to the speed of sound of the ambient gas.
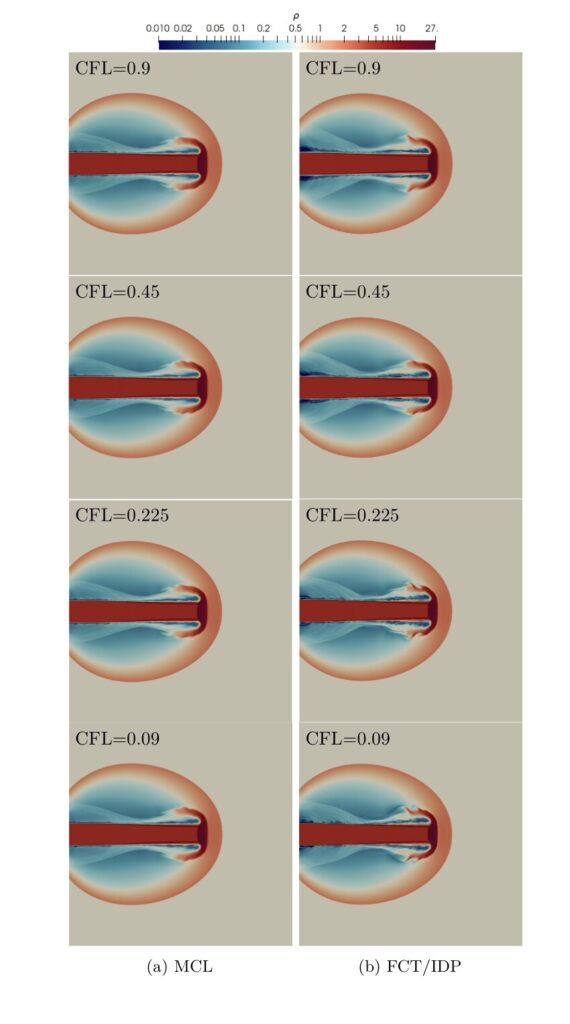
A spatial resolution of $256\times 256$ quadrilateral elements, a polynomial degree of $N=3$, and four different CFL numbers are used.
The simulations are stabilized by using two different subcell limiting approaches, the monolithic convex limiting (MCL) and the FCT/IDP limiting.
The resulting density contours at $t=10^{-3}$:
The dependence of the spatial discretization on the time-step size for FCT/IDP methods causes the number of vortical structures to be highly dependent on the CFL number and the total number of time steps to be not inversely proportional to the CFL number.
In fact, the amount of dissipation is reduced for small CFL numbers, which leads to lower minimum densities and higher maximum pressures in FCT/IDP, as can be seen in this Table.
References
[1] Rueda-Ramírez, A., Bolm, B., Kuzmin, D. & Gassner, G. (2023). Monolithic Convex Limiting for Legendre-Gauss-Lobatto Discontinuous Galerkin Spectral Element Methods. arXiv preprint arXiv:2303.00374 - Thesis Snapshot: A wet-dry treatment to numerically solve the shallow water equations with a high-order discontinuous Galerkin method with Trixi.jl (Master’s Thesis by Sven Goldberg) June 2, 2023
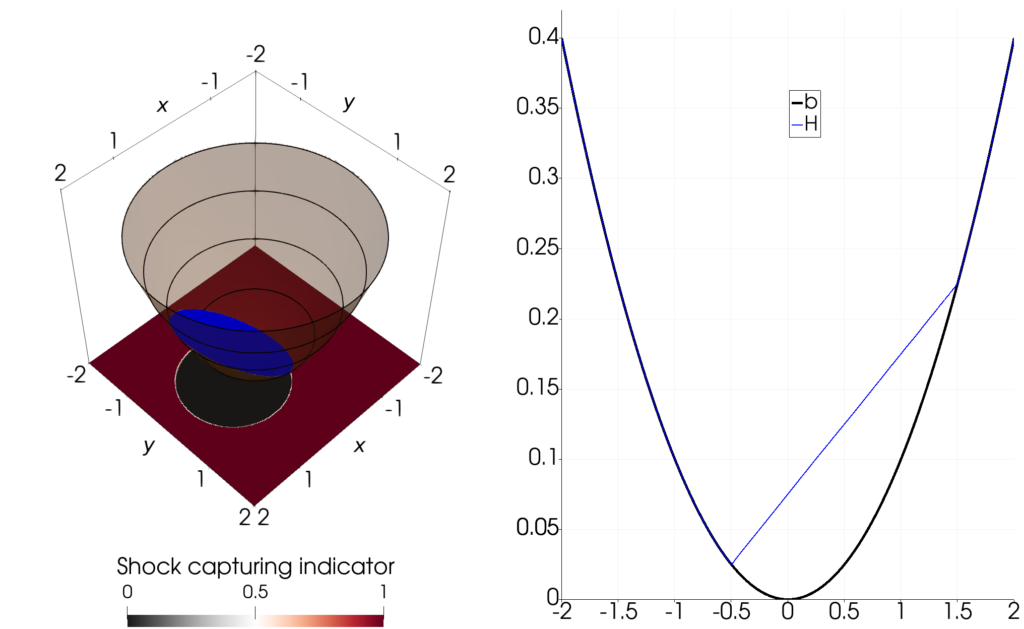
The shallow water equations are a well-known and often used physical model to simulate shallow water flow within given domains such as oceans. They are a system of hyperbolic partial differential equations and consist of conservation equations.
The numerical solver Trixi.jl is used to find approximate solutions to the equations. The shallow water equations are already embedded in this framework, but Trixi.jl does not yet allow for the appearance of dry sub-regions. Some strategies are combined and implemented to resolve the wet-dry problem resulting in a stable and well-balanced scheme: We use the positivity-preserving limiter by Zhang and Shu [1], the hydrostatic reconstruction method by Chen and Noelle [2] and a strategy to identify and mark dry cells.
A standard test exists to check for accuracy, namely the parabolic bowl test by Niklas Wintermeyer [3], first presented by William Thacker [4]. We use a StructuredMesh with 75625 elements and polynomial degree five. Since it has periodic analytical solutions, we can show the precision by realizing the initial state and its linear structure are recovered after one period. In the left picture, the whole domain is shown. In the right image, a slice at $y=0$ is visualized. Both are snapshots after one period:
We also use the TrixiBottomTopography.jl package by Maximilian Bertrand to account for real-world bottom topography data from the DGM1 data set. We give the simulation of flooding on the Rhine River valley using a TreeMesh with 1024 elements polynomial degree six and outflow boundary conditions:
References:
[1] Zhang, X. and Chi-Wang, S. (2011). Maximum-principle-satisfying and positivity-preserving high-order schemes for conservation laws: survey and new developments. Proc. R. Soc. A. 467:2752–2776. http://doi.org/10.1098/rspa.2011.0153
[2] Chen, G. and Noelle, S. (2017). A New Hydrostatic Reconstruction Scheme Based on Subcell Reconstructions. SIAM Journal on Numerical Analysis, 55, 758-784. https://doi.org/10.1137/15M1053074
[3] Wintermeyer, N.(2018). A novel entropy stable discontinuous Galerkin spectral element method for the shallow water equations on GPUs. Dissertation, Universität zu Köln. https://kups.ub.uni-koeln.de/9234/
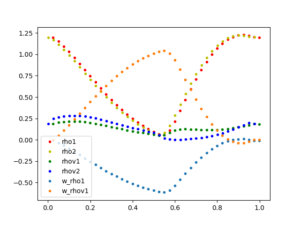
[4] Thacker, W. (1981). Some exact solutions to the nonlinear shallow-water wave equations. Journal of Fluid Mechanics, 107, 499-508. doi:10.1017/S0022112081001882 - Snapshot: Subcell limiting strategies for the DGSEM with Legendre–Gauss nodes May 4, 2023
The discontinuous Galerkin spectral element method (DGSEM) is a nodal discontinuous Galerkin collocation scheme that uses a set of Legendre-Gauss or Legendre-Gauss-Lobatto nodes to represent the solution with Lagrange interpolating polynomials and to compute integrals with a quadrature rule.
It was recently shown [1] that the DGSEM semi-discretization of a conservation law using Legendre-Gauss nodes can be written in finite-volume form as
\begin{equation*}
J_{j} \dot{\mathbf{u}}^{DG}_{j} =
\frac{1}{\omega_j}
\left(
\hat{\mathbf{f}}^{DG}_{(j-1,j)}
– \hat{\mathbf{f}}^{DG}_{(j,j+1)}
\right),
\end{equation*}
where $J_j$ is the mapping Jacobian, $\omega_j$ are the Legendre-Gauss quadrature weights, and $\hat{\mathbf{f}}^{DG}_{(\cdot,\cdot)}$ are high-order DGSEM fluxes between adjacent nodes.The existence of a FV form for the Legendre–Gauss DGSEM enables the use of the subcell limiting strategies described in [2]. In these methods, a hybrid DGSEM/FV method is used, where the semi-discretization at each node reads
\begin{equation*}
J_{j} \dot{\mathbf{u}}_{j} =
\frac{1}{\omega_j}
\left(
\hat{\mathbf{f}}_{(j-1,j)}
– \hat{\mathbf{f}}_{(j,j+1)}
\right),
\end{equation*}
and the local fluxes are obtained as a convex combination of high-order DGSEM and low-order FV fluxes,
\begin{equation*}
\hat{\mathbf{f}}_{(i,j)} = (1-\alpha_{(i,j)}) \hat{\mathbf{f}}^{DG}_{(i,j)}
+
\alpha_{(i,j)}
\hat{\mathbf{f}}^{DG}_{(i,j)},
~~~~
\alpha_{(i,j)} \in [0,1].
\end{equation*}To illustrate the shock-capturing capacity of the hybrid DGSEM/FV method, we simulate a Sedov blast problem describing the evolution of a blast wave expanding from an initial concentration of density and pressure, and adjust the blending coefficient $\alpha_{(i,j)}$ to avoid non-physical density oscillations in the vicinity of shocks.
The video shows the distribution of density and the blending coefficient obtained for entropy-stable variants of the Legendre-Gauss and Legendre-Gauss-Lobatto DGSEM methods.
The simulation runs stably without any spurious oscillations for both variants of the DGSEM method.
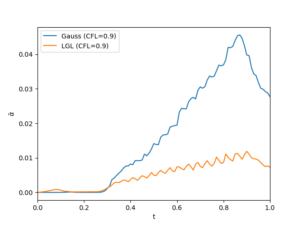
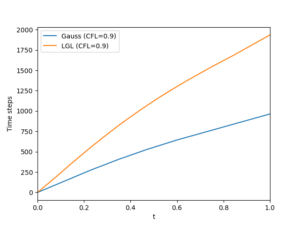
The figures below show the mean blending coefficient and the number of time steps for the simulation of the blast wave.
Although the Legendre–Gauss DGSEM requires more limiting than the Legendre-Gauss-Lobatto DGSEM to avoid spurious density oscillations, it completes the simulation in fewer time steps.
The Legendre-Gauss subcell distribution allows for longer time-step sizes than the Legendre-Gauss-Lobatto subcell distribution for the same CFL number.Figure 1: Evolution of the mean blending coefficient and number of time steps taken for the simulation of the blast wave with CFL=0.9.
References
[1] Mateo-Gabín, A., Rueda-Ramírez, A. M., Valero, E., & Rubio, G. (2022). Entropy-stable flux-differencing formulation with Gauss nodes for the DGSEM. arXiv preprint arXiv:2211.05066.
[2] Rueda-Ramírez, A. M., Pazner, W., & Gassner, G. J. (2022). Subcell limiting strategies for discontinuous Galerkin spectral element methods. Computers & Fluids, 247, 105627. arXiv preprint arXiv:2202.00576. - Snapshot: SPH simulation of spheres falling into a tank of water April 3, 2023
- New paper published: Reliable genotyping of recombinant genomes using a robust hidden Markov model April 3, 2023
Meiotic recombination is an essential mechanism during sexual reproduction and includes the exchange of chromosome segments between homologous chromosomes. New allelic combinations are transmitted to the new generation, introducing novel genetic variation in the offspring genomes. With the improvement of high-throughput whole-genome sequencing technologies, large numbers of recombinant individuals can now be sequenced with low sequencing depth at low costs, necessitating computational methods for reconstructing their haplotypes. The main challenge is the uncertainty in haplotype calling that arises from the low information content of a single genomic position. Straightforward sliding window-based approaches are difficult to tune and fail to place recombination breakpoints precisely. Hidden Markov Model-based approaches, on the other hand, tend to over-segment the genome. Here, we present RTIGER, an HMM-based model that exploits in a mathematically precise way the fact that true chromosome segments typically have a certain minimum length. We further separate the task of identifying the correct haplotype sequence from the accurate placement of haplotype borders, thereby maximizing the accuracy of border positions. By comparing segmentations based on simulated data with known underlying haplotypes, we highlight the reasons for RTIGER outperforming traditional segmentation approaches. We then analyze the meiotic recombination pattern of segregants of two Arabidopsis (Arabidopsis thaliana) accessions and a previously described hyper-recombining mutant. RTIGER is available as an R-package with an efficient Julia implementation of the core algorithm.
Plants Physiology: https://doi.org/10.1093/plphys/kiad191
- Snapshot: Test Simulation with novel wet/dry DG implementation February 22, 2023
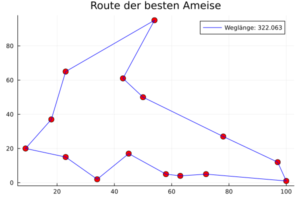
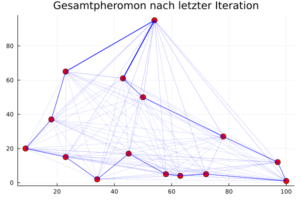
- Thesis Snapshot: Ameisenalgorithmen – Metaheuristische Verfahren zur Lösung des Travelling Salesman Problems (Bachelorarbeit von Marie Becker) February 3, 2023
In den neunziger Jahren wurden erstmals Ameisenalgorithmen von Marco Dorigo vorgestellt. Der erste Algorithmus war das sogenannte Ant System (AS), welches in der Bachelorarbeit implementiert wurde, um das Travelling Salesman Problem zu lösen. Dabei wird das Verhalten von Ameisen in einen Algorithmus übertragen, um den kürzesten Hamiltonkreis in einem Graphen zu finden. Die Ameisenalgorithmen bauen auf dem Prinzip auf, dass jede virtuelle Ameise, ausgehend von einem zufälligen Startknoten, einen Hamiltonkreis in dem gegebenen Graphen abläuft und auf dieser Tour dann Duftstoffe, sogenannte Pheromone, hinterlässt. Die hinterlassene Menge der Pheromone hängt dabei davon ab, wie lang die Tour einer Ameise ist. Durch die Duftstoffe werden andere Ameisen dazu angeregt, auch diesen Weg zu wählen. Je mehr Pheromone sich auf einer Kante befinden, desto wahrscheinlicher ist es, dass eine Ameise diese Kante in ihrer Tour wählt. Nach einigen Iterationen befindet sich also die größte Menge der Pheromone auf dem kürzesten Hamiltonkreis. Eine Erweiterung dieses Algorithmus ist das Ant Colony System (ACS), welches ebenfalls auf das Travelling Salesman Problem angewandt wurde. Einer der Unterschiede zum Ant System ist es, dass die Ameisen alle die gleiche Menge an Pheromonen auf ihrer Tour hinterlassen und außerdem die beste Ameise ausgewählt wird, welche eine zusätzliche Menge an Pheromonen auf ihrem Hamiltonkreis abgibt. Im Laufe der Jahre wurden weitere Modifikationen entwickelt, die sich auch auf andere Optimierungsprobleme anwenden lassen.
Abbildung: Beispiel für die Lösung des Travelling Salesman Problems mit dem ACS [1] M. Dorigo und T. Stuetzle, Ant Colony Optimization. MIT Press Ltd, 2004, isbn: 9780262042192
- New Open Position: Postdoc in Scientific Computing January 31, 2023
The Numerical Simulation group of Professor Gassner invites applications for a 2.5 year (possibility for extensions afterwards available) postdoc position in scientific computing (pay grade 100% TVL-13).
Deadline for applications is 10.2.2023.
For details, please have a look at the job ad: click here
For questions, please contact Professor Gassner via Email (ggassner@uni-koeln.de).
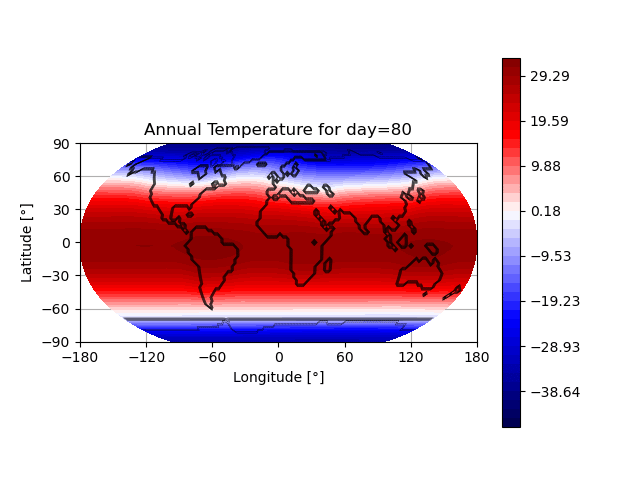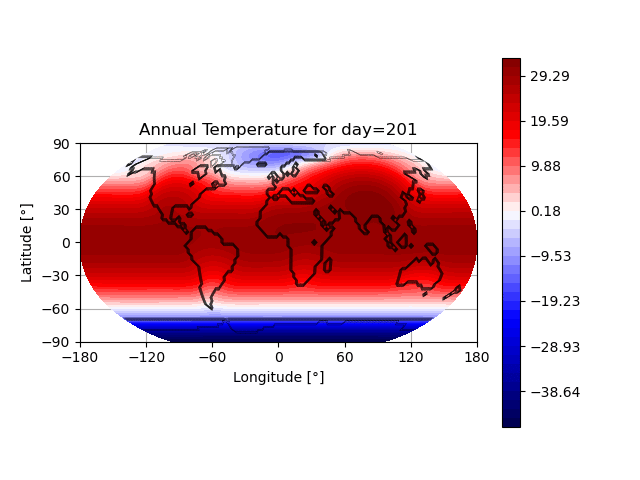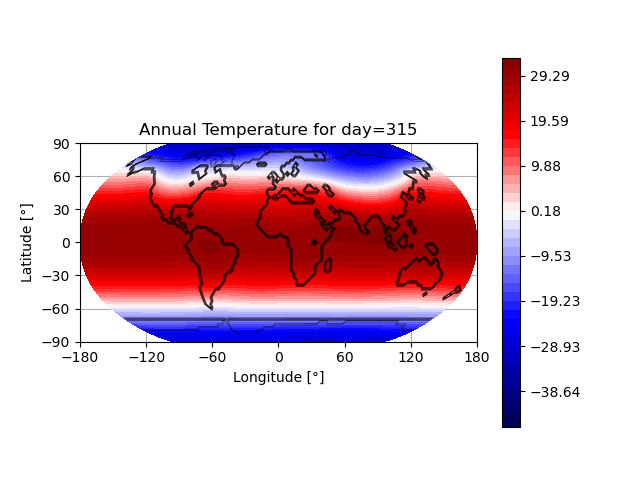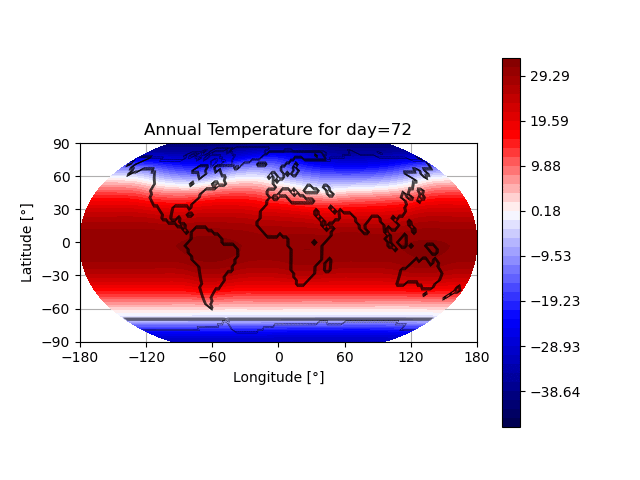
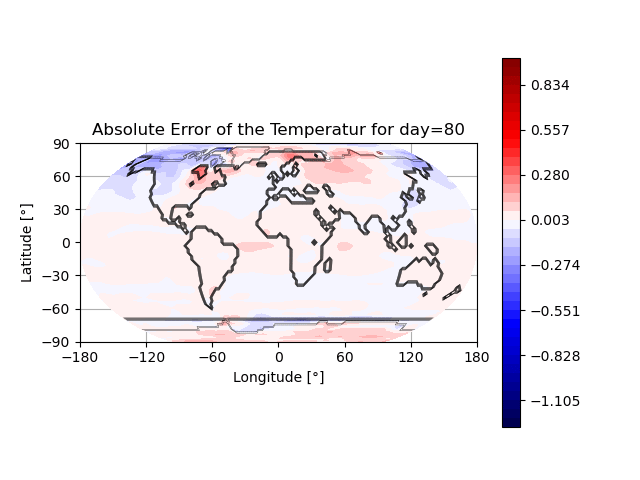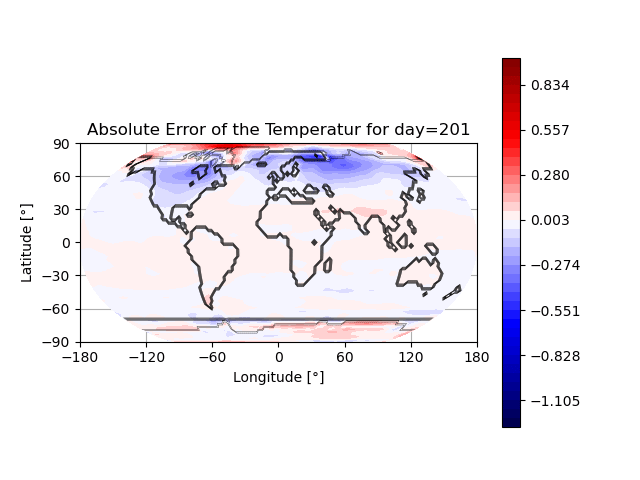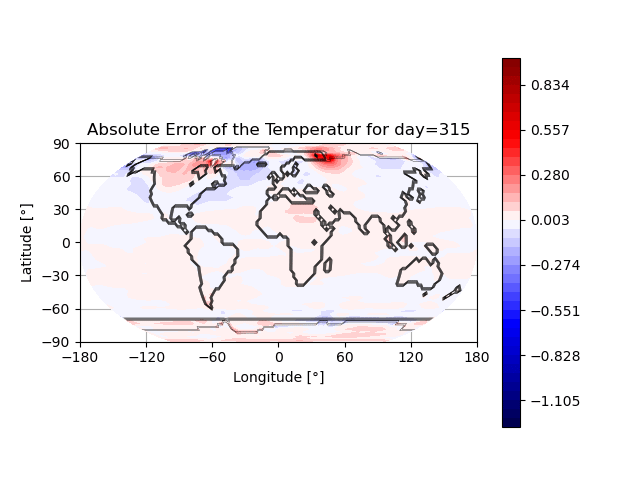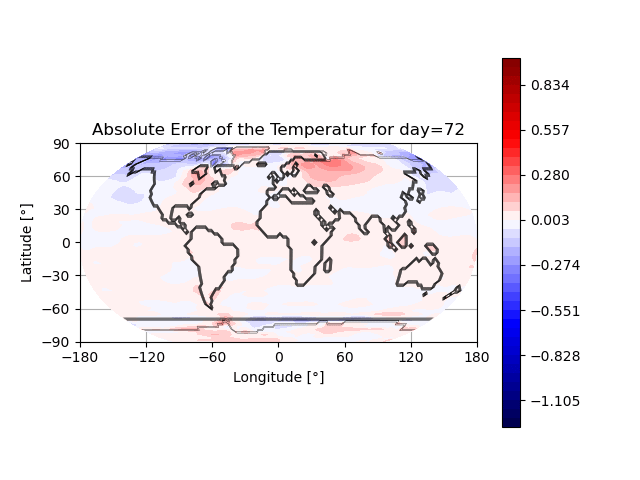
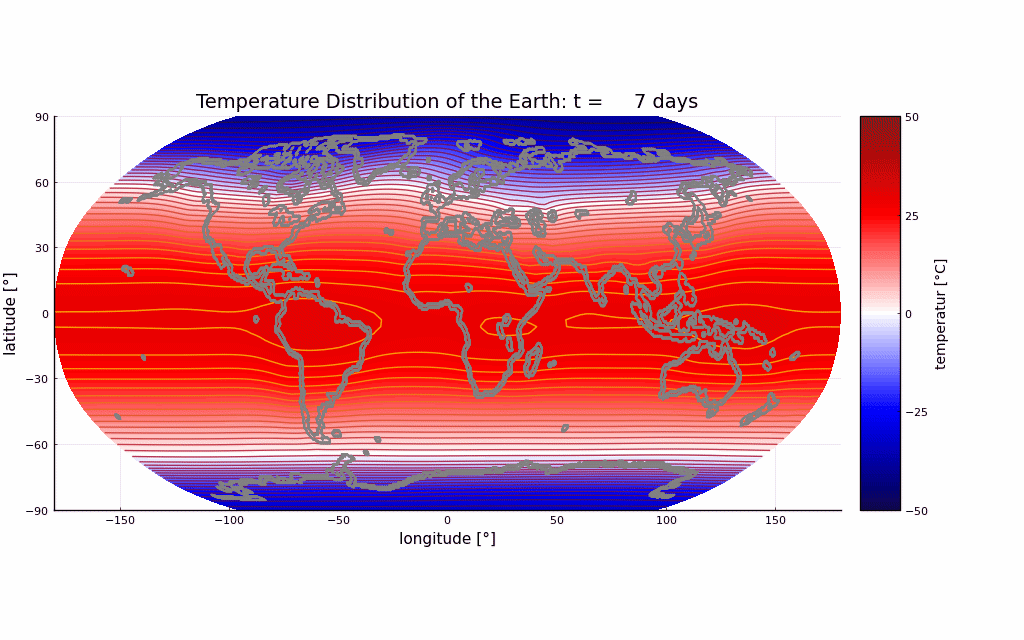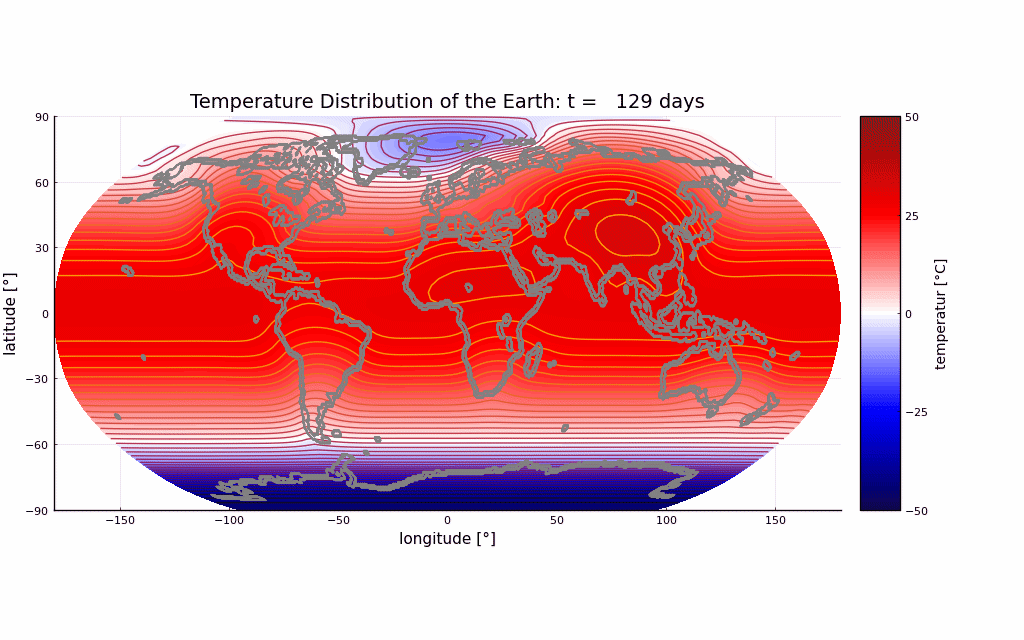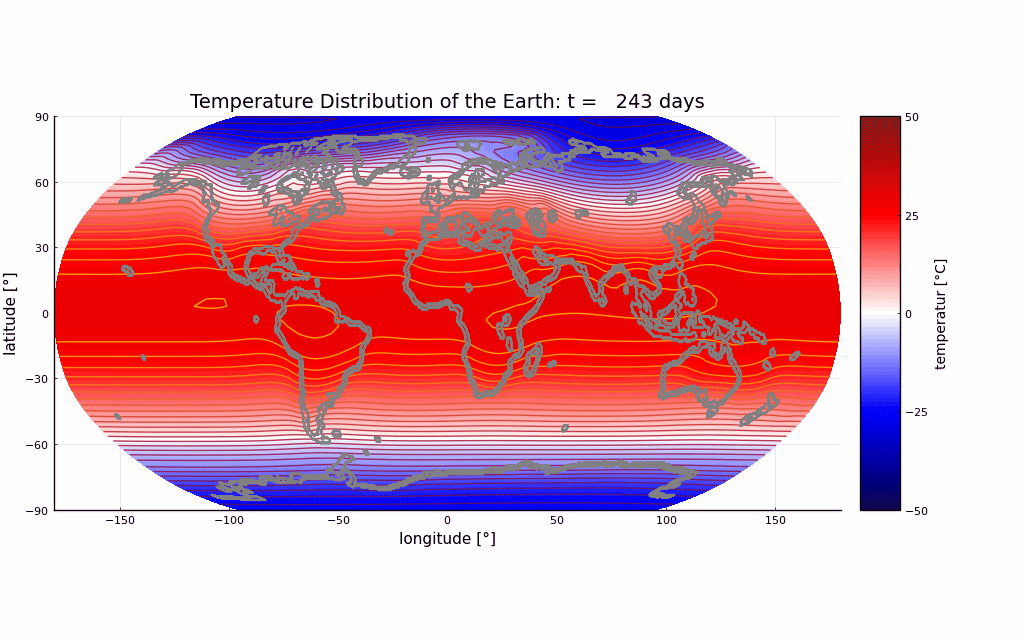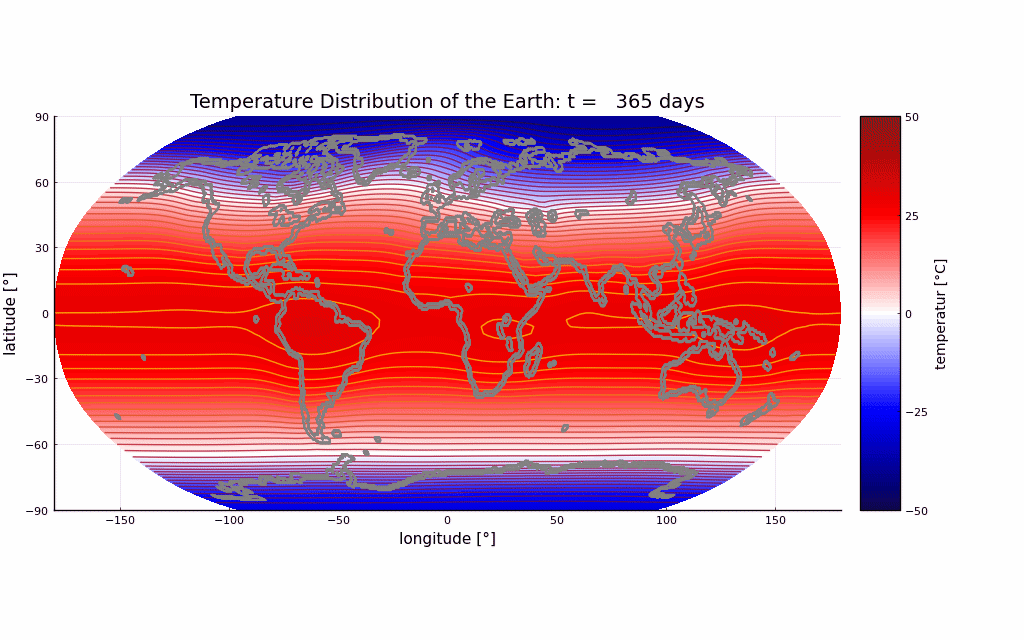
- Snapshot: Prediction of annual earth surface temperature with Fourier Neural Operator January 30, 2023
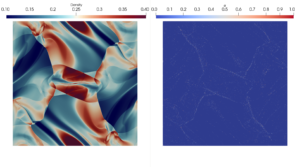
Recently, a lot of research has been done on the development of Neural Operators. The aim is to map infinite-dimensional functions to infinite-dimensional functions with neural networks. One approach is the Fourier Neural Operator [1]. We use this model to estimate the annual temperature based on the global land-sea-ice distribution. The input of the neural network is the earth’s geography, the output is the global temperature over one year. The training and testing data set is generated with the simulation framework “Klimakoffer” (for more information see Snapshot: Numerical simulations of earth’s climate and [2]).
The best results are achieved when using 4 Fourier integral operator layers, 16 Fourier modes, and a network width of 20. The model thus has 52 433 557 trainable parameters. The remaining specifications are as chosen by Li et al. [1]. It took 4 hours and 26 minutes to train the model on an NVIDIA GeForce RTX 3090 GPU and 0.77 seconds to evaluate it for one given example on a CPU. A relative L2 loss of approximately 0.0025 was achieved during training.
The first video shows one exemplary output. The second animation visualizes the difference between the temperature calculated by the FNO model and the “true” temperature determined by the framework “Klimakoffer”.
References:
[1] Li, Z., Kovachki, N., Azizzadenesheli, K., Liu, B., Bhattacharya, K., Stuart, A., Anandkumar, A. (2020). “Fourier Neural Operator for Parametric Partial Differential Equations”, arXiv, https://arxiv.org/abs/2010.08895
[2] Zhuang, K., North, G.R., Stevens, Mark J. (2017). “A NetCDF version of the two-dimensional energy balance model based on the full multigrid algorithm”, SoftwareX - Thesis Snapshot: Bottom topography modelling for the shallow water equations in Trixi.jl (Master’s thesis by Maximilian Bertrand) December 22, 2022
Back in the summer of 2021, severe floods struck Western Germany, resulting in several cities and villages being destroyed and hundreds of people losing their lives. Modelling and predicting those floods can be crucial for investigating such natural disasters. The shallow water equations are a system of physical conservation equations that can model water flow over a given domain. The two dimensional shallow water equations are given as follows:
\begin{equation*}
\left\{\begin{aligned}
\frac{\partial}{\partial t} h + \left( h v_1\right)_x + \left( h v_2\right)_y =0&\\
\frac{\partial}{\partial t} hv_1 + \left( hv_1^2 + \frac{1}{2} gh^2\right)_x + \left(h v_1v_2\right)_y &= -ghb_x\\
\frac{\partial}{\partial t}h v_2 + \left( hv_1v_2\right)_x + \left(hv_2^2 +\frac{1}{2} gh^2\right)_y &= -ghb_y
\end{aligned}\right.
\end{equation*}Here the variable $b$ describes the underlying bottom topography function of the domain. As this system is set up of hyperbolic partial differential equations, we use the numerical solver Trixi.jl to approximate the solutions. This solver is part of the trixi-framework. Trixi.jl already implemented the shallow water equations but did not yet offer the functionality to include real-world topography data into the calculations. Therefore the add-on TrixiBottomTopography.jl has been included in the trixi-framework. This tool uses B-spline interpolation approaches to remodel the bottom topography function from real-world data, which is often given as elevation data at specific points. One example is the DGM1 data set which provides uniformly spaced elevation data of the whole German state of North Rhine-Westphalia. Using this data set and the functionalities implemented in Trixi.jl as well as TrixiBottomTopography.jl, we can simulate a dam break problem over a section of the Rhine river valley.
- Talk: Gregor Gassner (UoC) with Robust Split-Form DGSEM for Hydro- and Magnetohydrodynamics December 13, 2022
In this talk, we present the class of split form discontinuous Galerkin methods. The notion of split form refers to different interpretations of the non-linear terms in the fluid dynamics equations. For instance the advective part of the momentum flux can be cast in analytically equivalent forms such as the advective form, or the conservative form, or convex combinations of both forms. While these forms are analytically equivalent for smooth solutions, it is interesting to understand that their discrete forms might have strongly different properties. It turns out that specific underlying split forms of the fluid equations give discontinuous Galerkin (DG) approximations with special favourable properties such as, kinetic energy preservation, energy consistency, pressure equilibrium preservation and even entropy conservation/stability. The most important improvement that can be observed is drastically increased non-linear robustness of the DG discretization, in particular when simulating under-resolved turbulence. A necessary ingredient to retain fully discrete conservation when using split formulations is the so-called summation-by-parts (SBP) property of the discrete derivative and integral operator. It turns out hat specific DG discretizations, such as the Legendre-Gauss-Lobatto (LGL) spectral element method, satisfy the SBP property. We will further discuss in this talk that it is possible to construct compatible low-order finite volume discretizations on the LGL subcell grid, such that a convex blending of the high-order DG method with the robust low-order method is feasible. This allows to construct provably positive hybrid discretizations that enable simulations of problems with strong shock waves, such as e.g. an astrophysical jet with Ma=2000.
Link to the Talk: https://cassyni.com/events/VrFL7HmR9YjHyFJvFcZNjP
- Snapshot: Dam break against a flexible structure with Smoothed Particle Hydrodynamics December 10, 2022
To simulate elastic structures, we use a total Lagrangian SPH formulation [1].
We simulate a dam break against a flexible structure based on the setup given by [1].
For the fluid dynamics, a weakly-compressible Lagrangian SPH formulation with an artificial viscosity by Monaghan [2] and boundary force particles to model the tank [3] was used.
This animation shows the simulation in 0.1x real time with 8.7k fluid particles and 455 particles to model the flexible structure.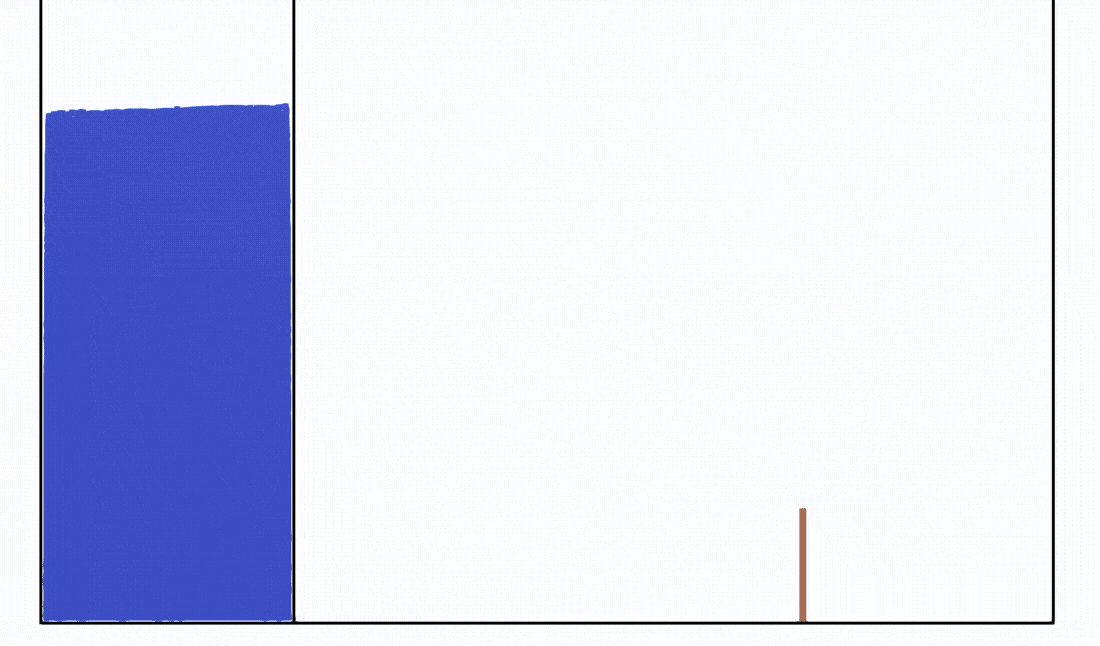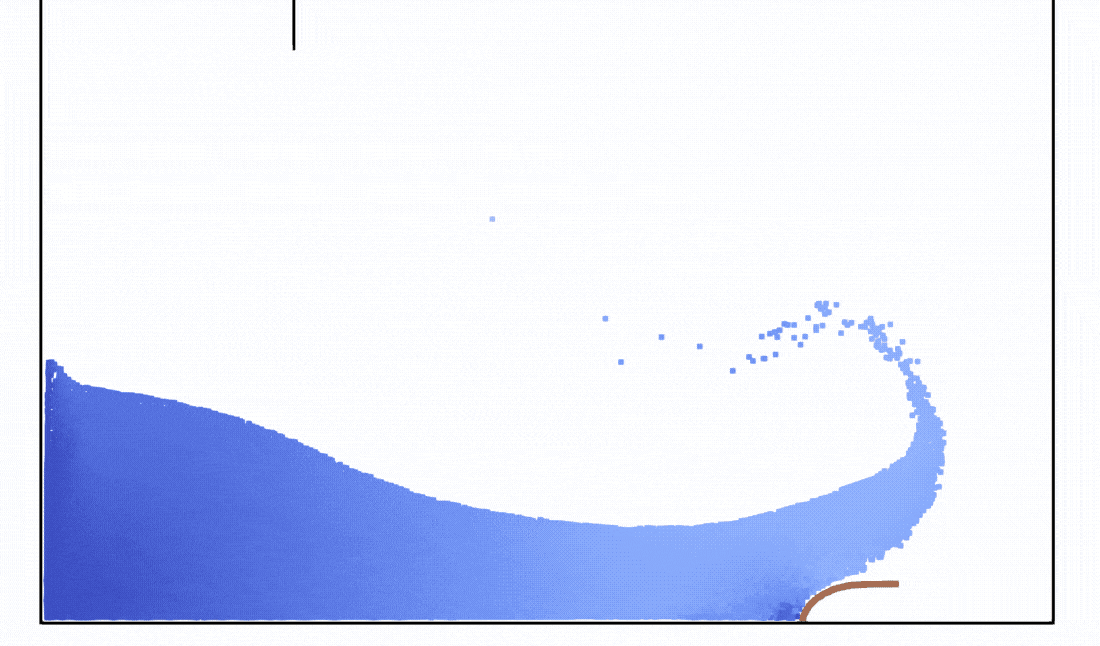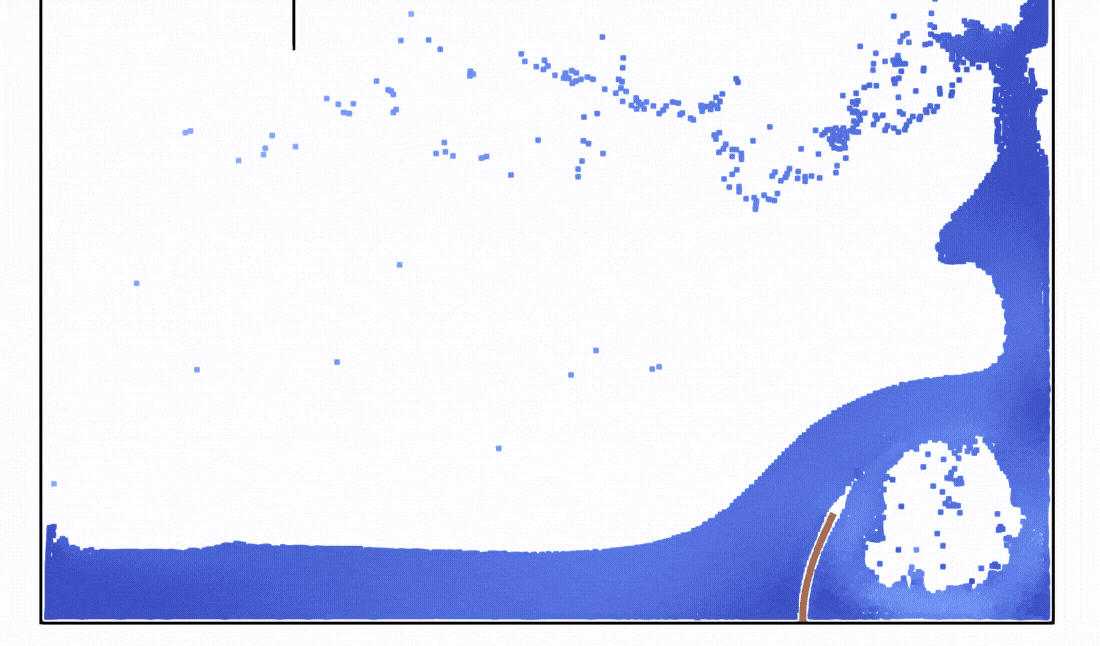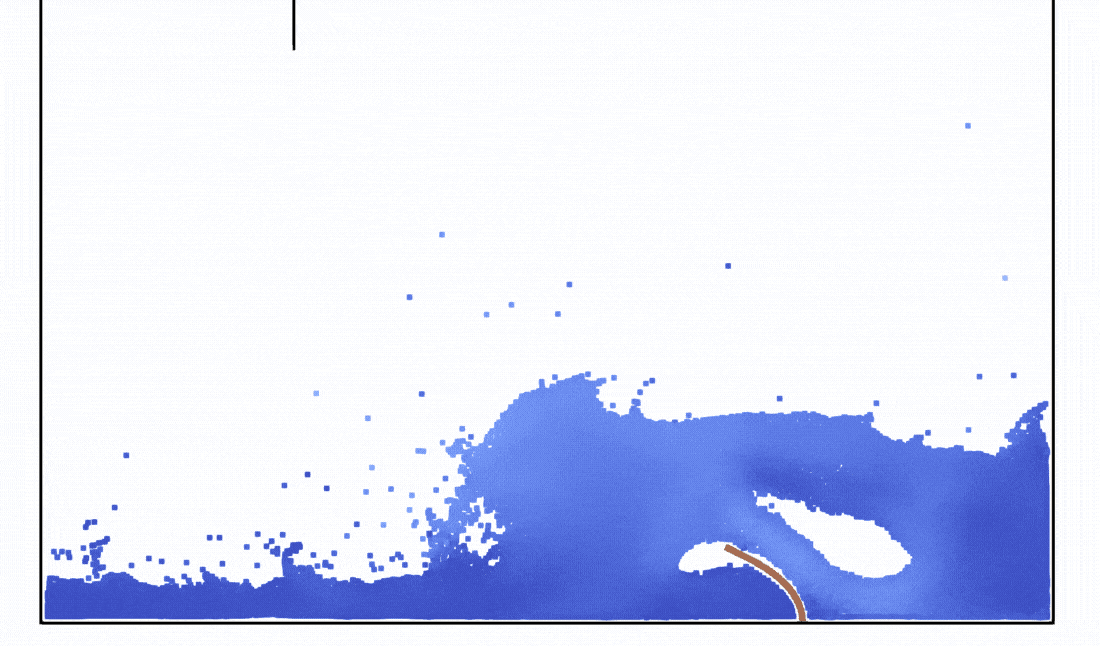
References:
[1] O’Connor, J., Rogers, B. D. (2021). “A fluid–structure interaction model for free-surface flows and flexible structures using smoothed particle hydrodynamics on a GPU.” In: Journal of Fluids and Structures, 104. https://doi.org/10.1016/J.JFLUIDSTRUCTS.2021.103312
[2] Monaghan, J. J. (1989). “On the Problem of Penetration in Particle Methods”. In: Journal of Computational Physics, 82(1), 1–15. https://doi.org/10.1016/0021-9991(89)90032-6
[3] Monaghan, J. J., & Kajtar, J. B. (2009). “SPH particle boundary forces for arbitrary boundaries”. In: Computer Physics Communications, 180(10), 1811–1820. https://doi.org/10.1016/j.cpc.2009.05.008 - Workshop: Novel Adaptive Discontinuous Galerkin Approaches for the Simulation of Atmospheric Flows November 11, 2022
On November 30th and December 1st, the workshop on “Novel Adaptive Discontinuous Galerkin Approaches for the Simulation of Atmospheric Flows” will take place at the Department of Mathematics and Computer Science with researchers from the German Aerospace Center (DLR) Cologne, Deutscher Wetterdienst (DWD), and University of Cologne (UoC). This workshop is supported by and embedded into the Center for Earth System Observation and Computational Analysis (CESOC).
The idea of the workshop is to discuss novel developments for discontinuous Galerkin methods applied to atmospheric flow simulations, with a focus on implicit time integration, meshing of the sphere, adaptivity, efficient implementations, benchmark test cases for atmospheric flows, entropy-stable split formulations of the nonlinear partial differential equations, and bounds-preserving numerical schemes.
A detailed program with abstracts is available here.
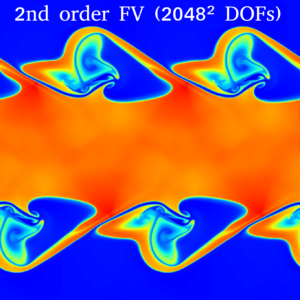
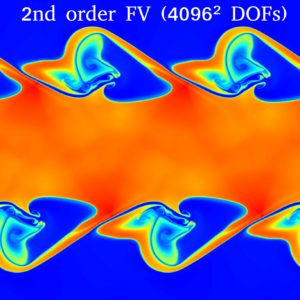
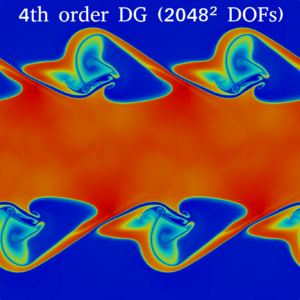
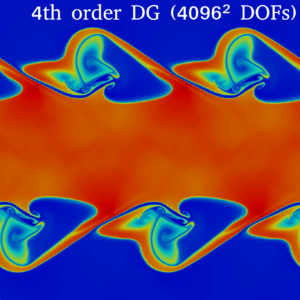
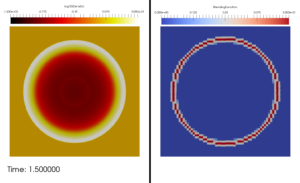
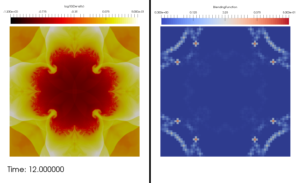
- Snapshot: High Mach number Kelvin-Helmholtz instability with DG and subcell positivity limiter November 8, 2022
We solve the compressible Euler equations of gas dynamics with a fourth-order accurate entropy-stable discontinuous Galerkin (DG) method and combine it with a first-order accurate finite volume (FV) method at the node level to impose positivity of density and pressure [1,2].
The initial condition of this problem is given by:
\[
\begin{array}{rlrl}
\rho (t=0) &= \frac{1}{2}
+ \frac{3}{4} B,
&
p (t=0) &= 0.1, \\
v_1 (t=0) &= \frac{1}{2} \left( B-1 \right),
&
v_2 (t=0) &= \frac{1}{10} \sin(2 \pi x),
\end{array}
\]
with $B=\tanh \left( 15 y + 7.5 \right) – \tanh(15y-7.5)$, where $\rho$ is the density, $\vec{v}=(v_1,v_2)$ is the velocity, and $p$ is the pressure.The video shows the evolution of the density in time using $1024^2$ and degrees of freedom. We use the entropy-conservative and kinetic energy preserving flux of Ranocha [3] for the volume fluxes and the Rusanov solver for the surface fluxes of the DG and FV methods. During this simulation, the FV method acts on average in 0.000086% of the computational domain, and never more than 0.002% of the computational domain at a specific time.
References
[1] A. M. Rueda-Ramírez, G. J. Gassner, A Subcell Finite Volume Positivity-Preserving Limiter for DGSEM Discretizations of the Euler Equations, WCCM-ECCOMAS2020, pp. 1–12.
[2] A. M. Rueda-Ramírez, W. Pazner, G. J. Gassner, Subcell limiting strategies for discontinuous galerkin spectral element methods, Computers & Fluids 247 (2022) 105627.
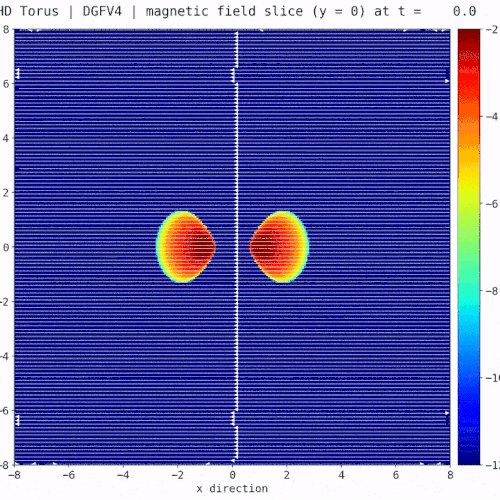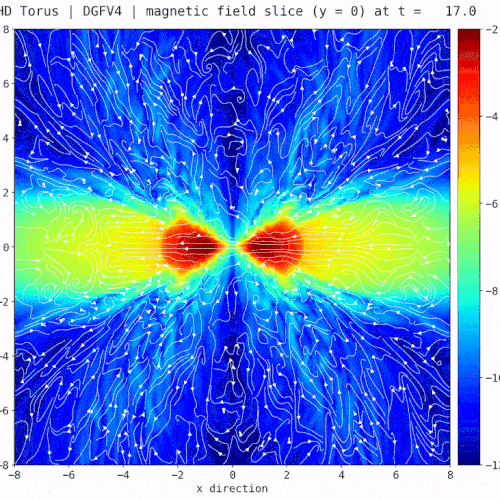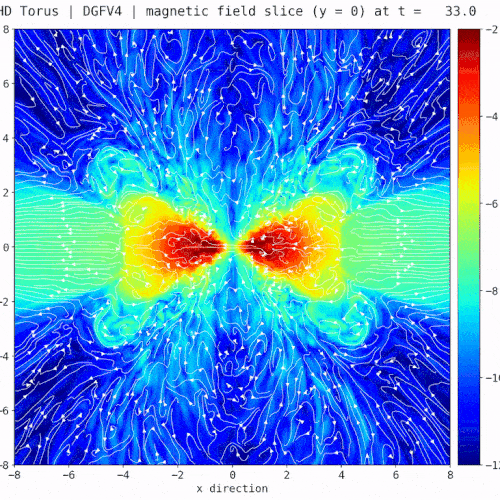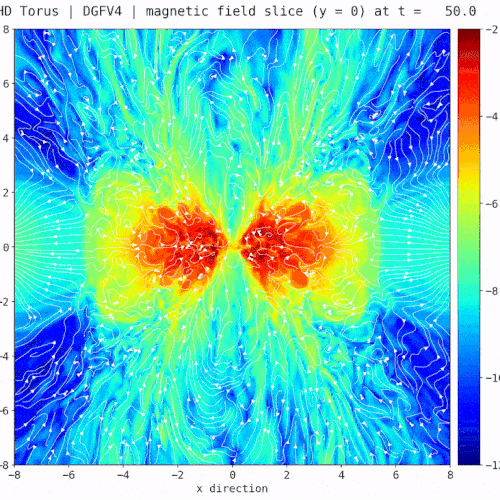
[3] H. Ranocha, Generalised summation-by-parts operators and entropy stability of numerical methods for hyperbolic balance laws, Cuvillier Verlag, 2018. - Snapshot: Multi-component magneto-hydrodynamics simulations with a bounds-preserving discontinuous Galerkin method October 4, 2022
We solve the multi-component magneto-hydrodynamics (MHD) equations using a hybrid finite volume (FV)/discontinuous Galerkin (DG) method [1], which combines the two discretization approaches at the node level. To test the robustness of the hybrid FV/DG method, we compute a modification of the Orszag-Tang vortex problem [2], where we use two ion species and initialize the flow with a sharp interface at $y=0$:
\[
\begin{array}{rlrl}
\rho^1(x,y,t=0) &= \begin{cases}
{25}/{36 \pi} & y \ge 0 \\
10^{-8} & y < 0
\end{cases} ,
&\rho^2(x,y,t=0) &= \begin{cases}
10^{-8} & y < 0\\
{25}/{36 \pi} & y \ge 0
\end{cases} , \\
v_1 (x,y,t=0) &= – \sin (2 \pi y),
&v_2 (x,y,t=0) &= \sin (2 \pi x), \\
B_1 (x,y,t=0) &= -\frac{1}{\sqrt{4 \pi}} \sin (2 \pi y),
&B_2 (x,y,t=0) &= -\frac{1}{\sqrt{4 \pi}} \sin (4 \pi x). \\
p (x,y,t=0) &= \frac{5}{12 \pi},
& & \\
\end{array}
\]
where $\rho^1$ is the density of the first ion species, $\rho^2$ is the density of the second ion species,$\vec{v}=(v_1,v_2)$ is the plasma velocity, $\vec{B}=(B_1,B_2)$ is the magnetic field, and $p$ is the plasma pressure (without magnetic pressure).
The fourth-order DG method delivers high accuracy, but fails to describe shocks and material interfaces. Therefore, we use a modal indicator [3] to detect the elements where the solution changes abruptly. In those elements, we combine the DG method with a robust lower order FV scheme locally (at the node level) to impose TVD-like conditions on the density of the ion species,
\[
\min_{k \in \mathcal{N} (j)} {\rho}^{i,\mathrm{FV}}_{k}
\le \rho^i_{j} \le
\max_{k \in \mathcal{N} (j)} {\rho}^{i,\mathrm{FV}}_{k},
\]
and a local minimum principle on the specific entropy,
\[
s({\mathbf{u}}_{j}) \ge \min_{k \in \mathcal{N} (j)} s(\mathbf{u}^{\mathrm{FV}}_{k}),.
\]
where $\mathcal{N} (j)$ denotes the collection of nodes in the low-order stencil of each node $j$.
The video shows the total density ($\rho=\rho^1+\rho^2$), the density of the first ion species ($\rho^1$), and the so-called blending coefficient ($\alpha$) for the combination of a fourth-order accurate entropy stable DG method with first- and second-order accurate FV methods (Rusanov solver) and $1024^2$ degrees of freedom. A blending coefficient $\alpha=0$ means that only the DG is being used, and a blending coefficient $\alpha=1$ means that only the FV method is being used. The example shows that the hybrid FV/DG scheme is able to capture the shocks of the simulation correctly, deal with near-vacuum conditions and sharp interfaces.[1] Rueda-Ramírez, A. M.; Pazner, W., & Gassner, G. J. (2022). Subcell limiting strategies for discontinuous Galerkin spectral element methods. Computers & Fluids. arXiv:2202.00576.
[2] Orszag, S.; Tang, C (1979). Small-scale structure of two-dimensional magnetohydrodynamic turbulence. Journal of Fluid Mechanics.
[3] Persson, P. O.; Peraire, J. (2006). Sub-cell shock capturing for discontinuous Galerkin methods. In 44th AIAA Aerospace Sciences Meeting and Exhibit (p. 112). - Snapshot: Dam break simulation with Smoothed Particle Hydrodynamics August 29, 2022
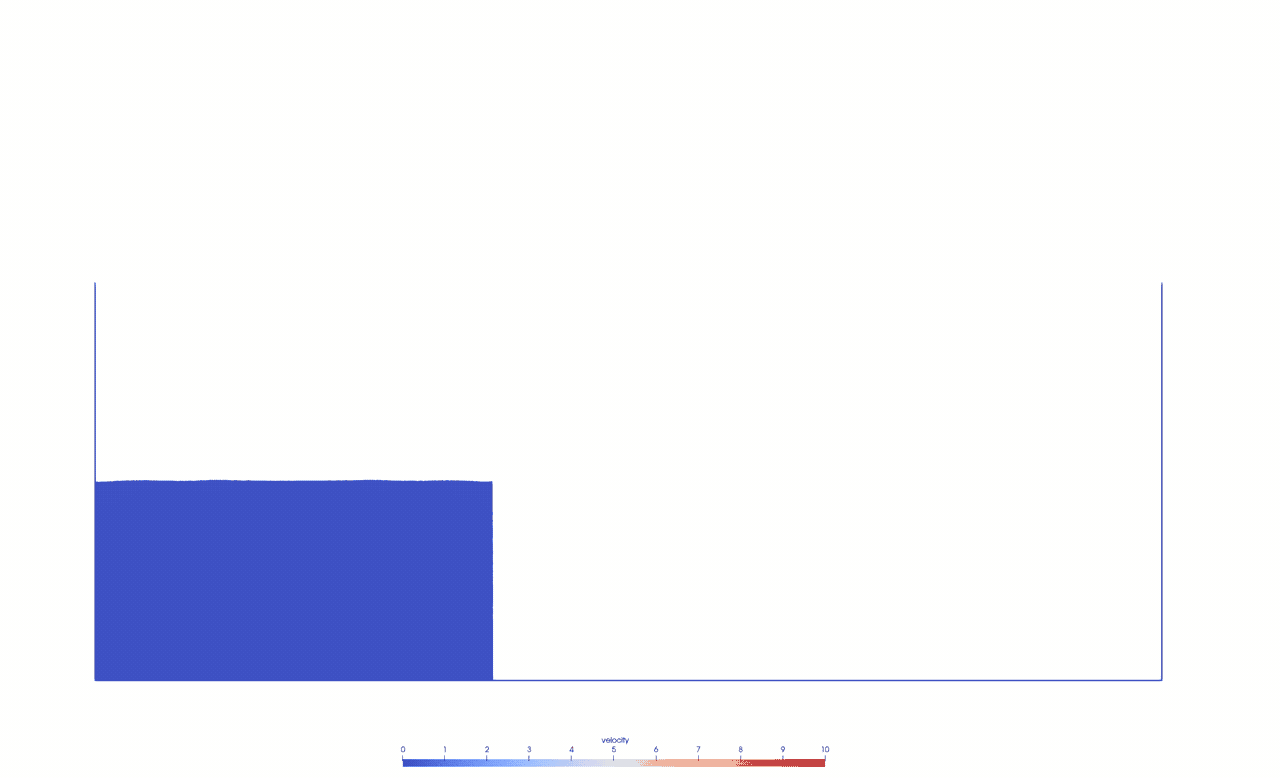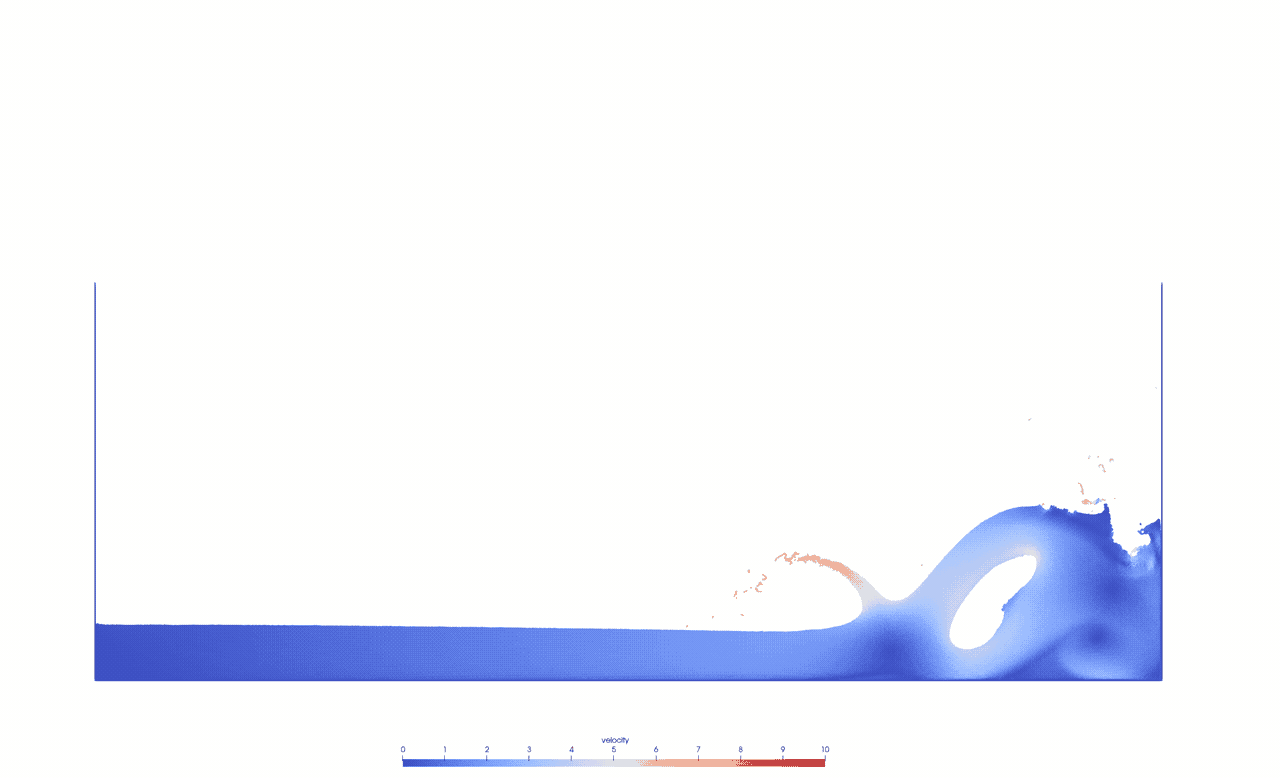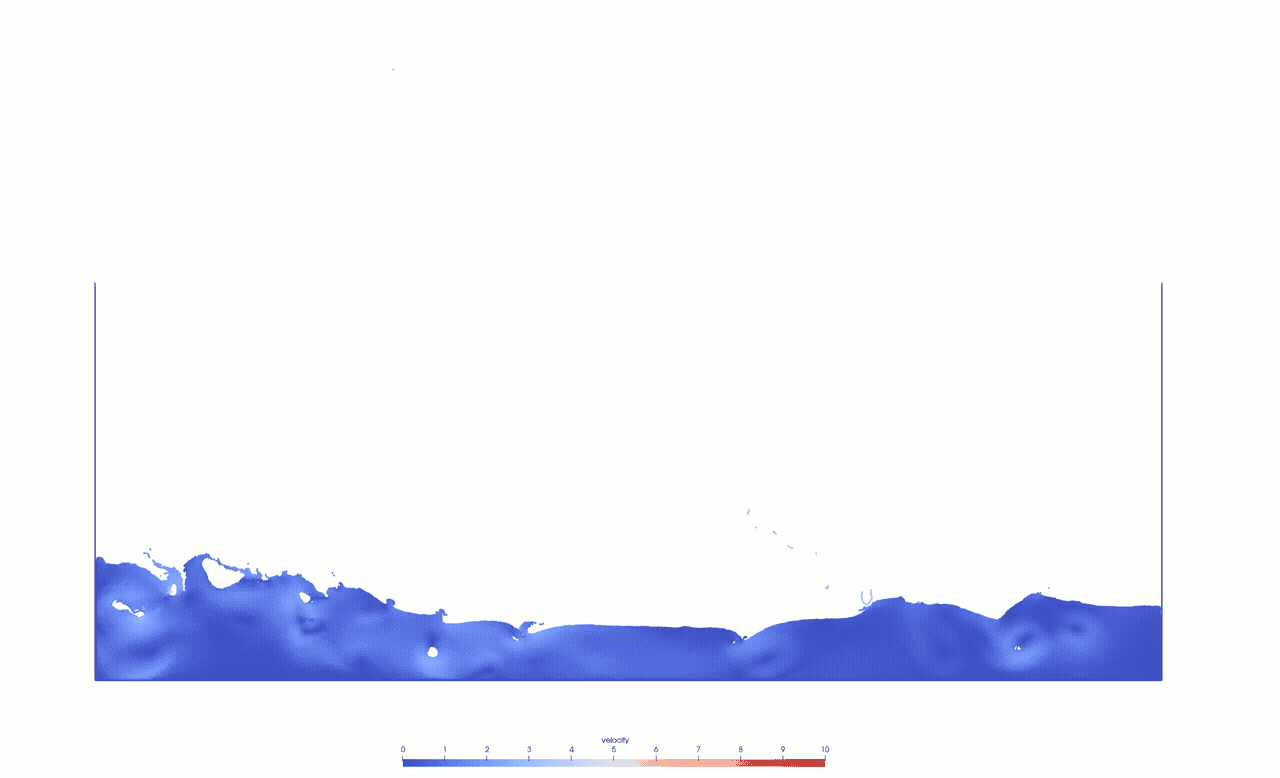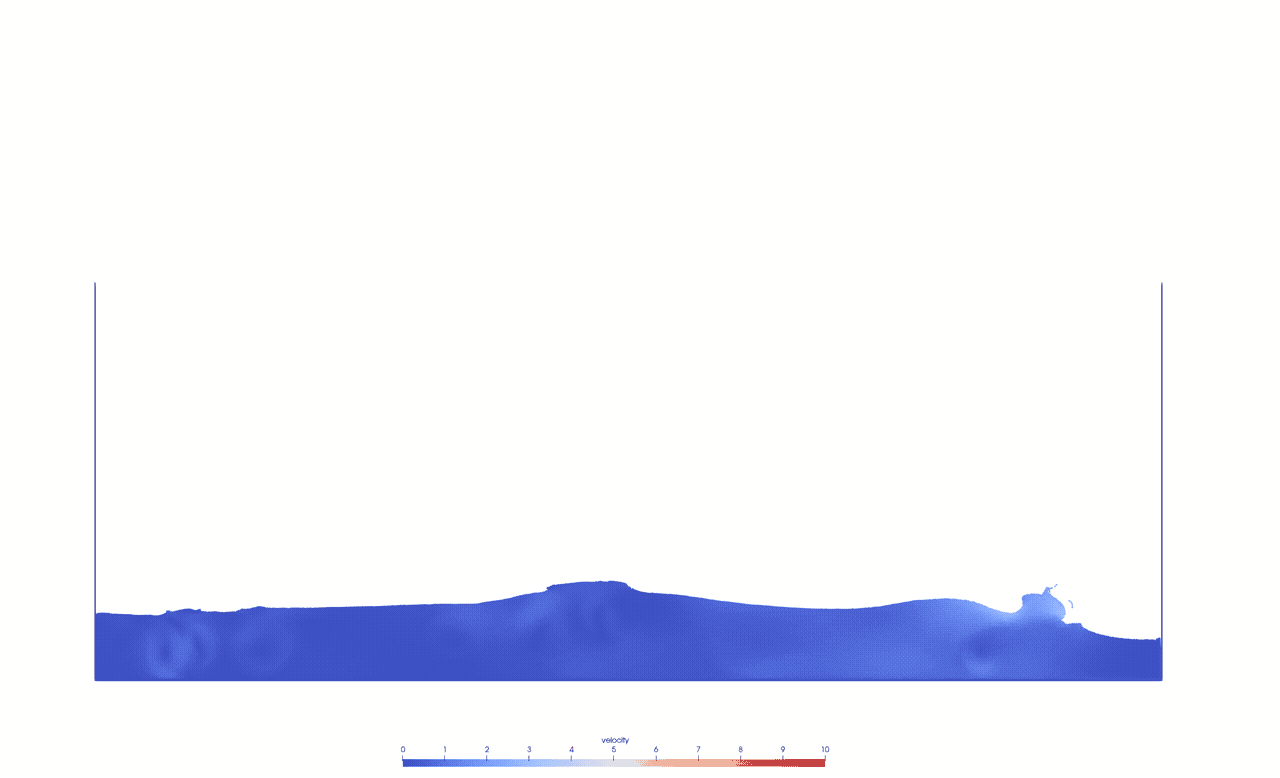
To study the Smoothed Particle Hydrodynamics method, we simulate a dam break based on the setup given by [1].
We use a weakly-compressible Lagrangian SPH formulation with an artificial viscosity by Monaghan [2] and boundary force particles to model the tank [3].This animation shows the simulation in 0.5x real time with 125k fluid particles and 7k boundary particles.
References:
[1] Marrone, S., Antuono, M., Colagrossi, A., Colicchio, G., le Touzé, D., & Graziani, G. (2011). “δ-SPH model for simulating violent impact flows”. In: Computer Methods in Applied Mechanics and Engineering, 200(13–16), 1526–1542. https://doi.org/10.1016/J.CMA.2010.12.016
[2] Monaghan, J. J. (1989). “On the Problem of Penetration in Particle Methods”. In: Journal of Computational Physics, 82(1), 1–15. https://doi.org/10.1016/0021-9991(89)90032-6
[3] Monaghan, J. J., & Kajtar, J. B. (2009). “SPH particle boundary forces for arbitrary boundaries”. In: Computer Physics Communications, 180(10), 1811–1820. https://doi.org/10.1016/j.cpc.2009.05.008 - Talk: Deniz Bezgin (TUM) and Aaron Buhendwa (TUM) about Differentiable Fluid Dynamics in JAX: Challenges and Perspectives, Friday, 26th August 2022, 10am CEST August 23, 2022
JAX-FLUIDS is a CFD solver written in Python, which uses the JAX framework to enable automatic differentiation (AD). This allows one to easily create applications for data-driven simulations or other optimization problems.The talk is based on the recent preprint “JAX-FLUIDS: A fully-differentiable high-order computational fluid dynamics solver for compressible two-phase flows” (arXiv:2203.13760).
To obtain the Zoom link for this online talk, please get in touch with Gregor Gassner or Michael Schlottke-Lakemper.
- Snapshot: Chaotic behavior of the Kelvin-Helmholtz Instability June 10, 2022
We investigate the Kelvin-Helmholtz instability setup of Fjordholm et al. [1], where the sharp interface in the initial condition is randomly perturbed. The simulation is done with an entropy stable DGSEM with polynomial degree N=3 and 32 x 32 grid cells. The final time is t = 2.0. Trixi.jl [2] is used with the setup found in examples/tree_2d_dgsem/elixir_euler_kelvin_helmholtz_instability_fjordholm_etal.jl.
The following gif is showing 100 simulation results of the density distribution for different random interface perturbations:
Here is the average density distribution of all 100 results:
[1] Ulrik S. Fjordholm, Roger Käppeli, Siddhartha Mishra, Eitan Tadmor. Construction of approximate entropy measure valued solutions for hyperbolic systems of conservation laws, 2014. (https://arxiv.org/abs/1402.0909)
[2] Trixi.jl, a numerical simulation framework for hyperbolic conservation laws written in Julia. (https://github.com/trixi-framework/Trixi.jl) - Thesis Snapshot: Planning of collision-free trajectories for UAVs and optimization using uniform B-splines. (Bachelor thesis by Alexander Bast) May 10, 2022
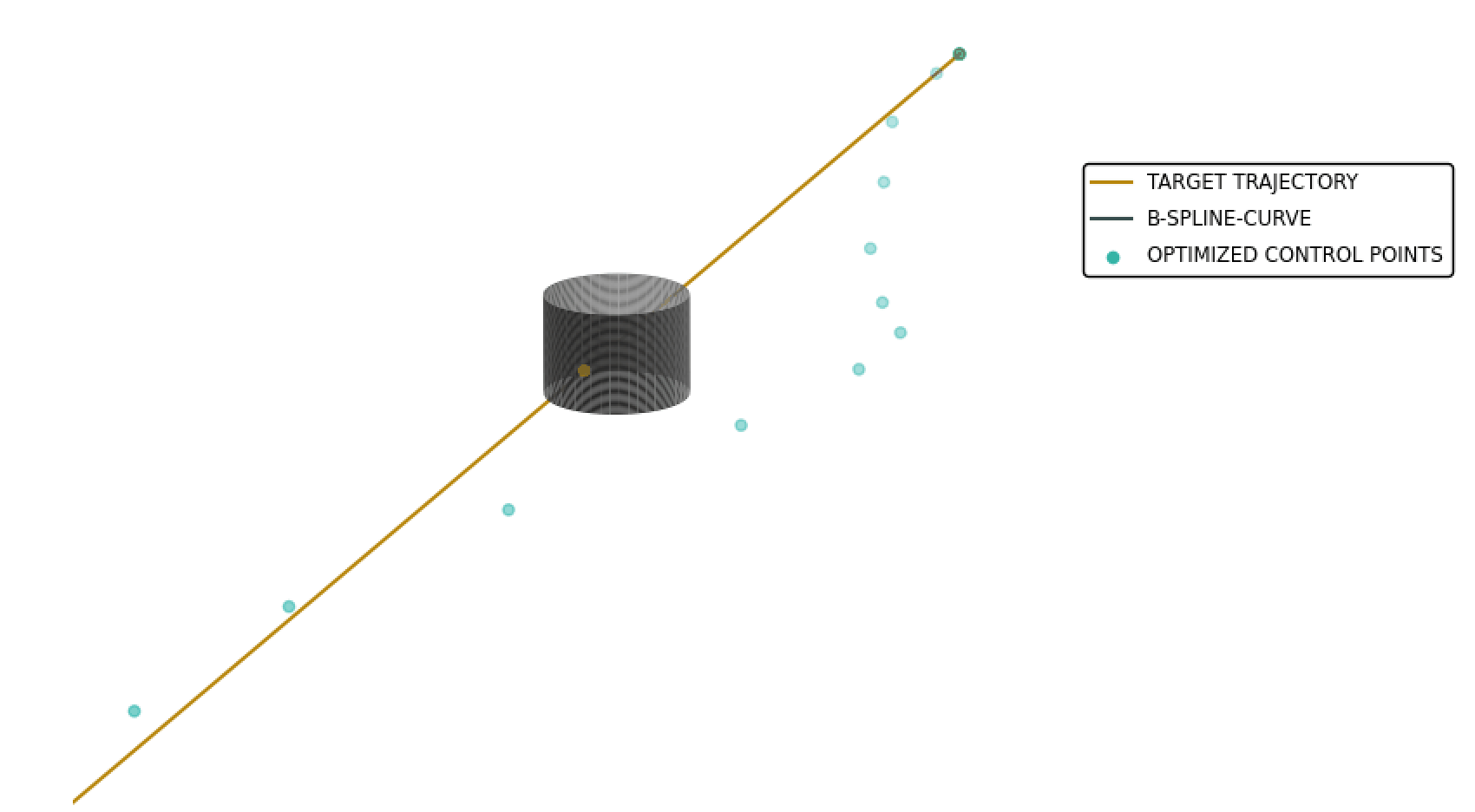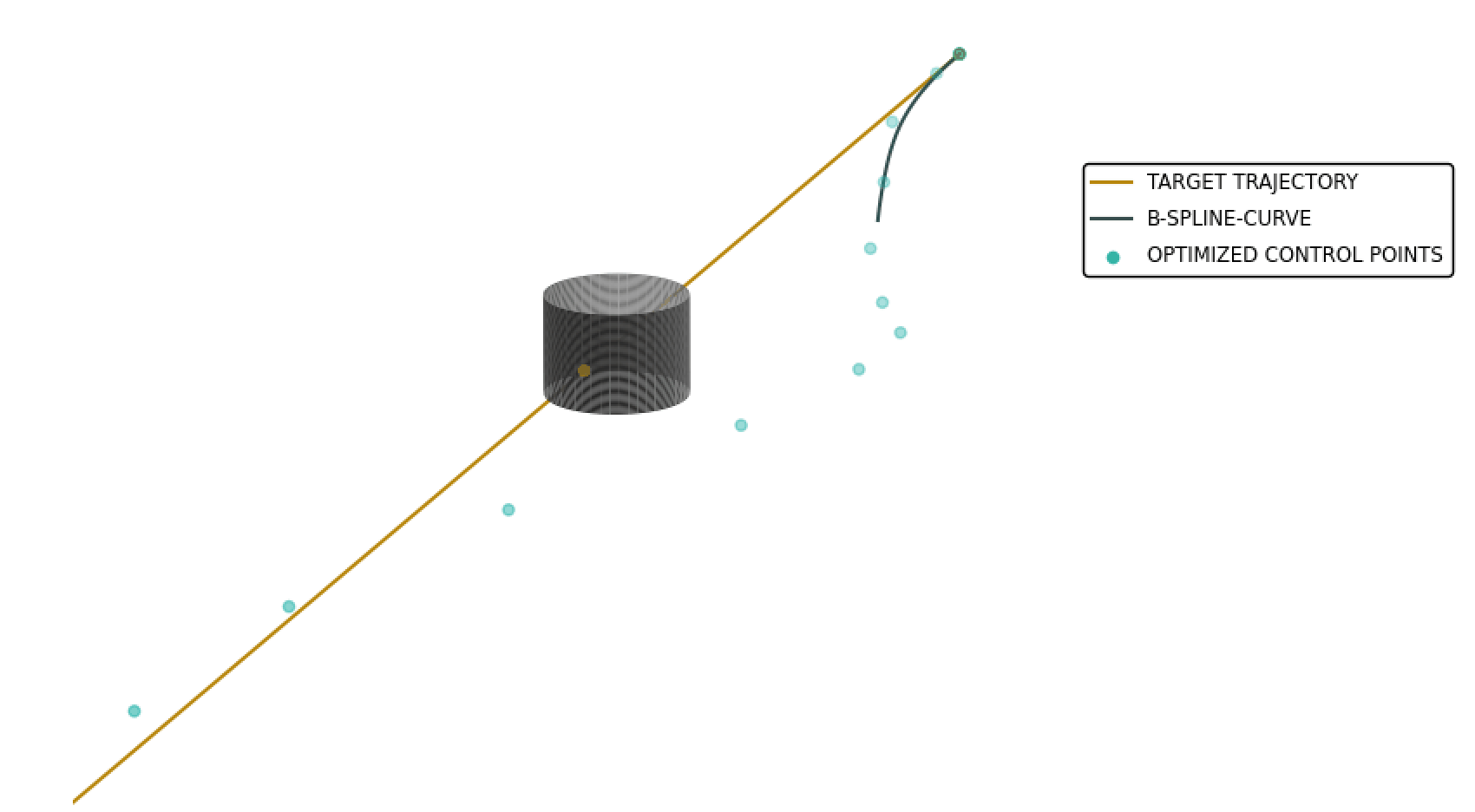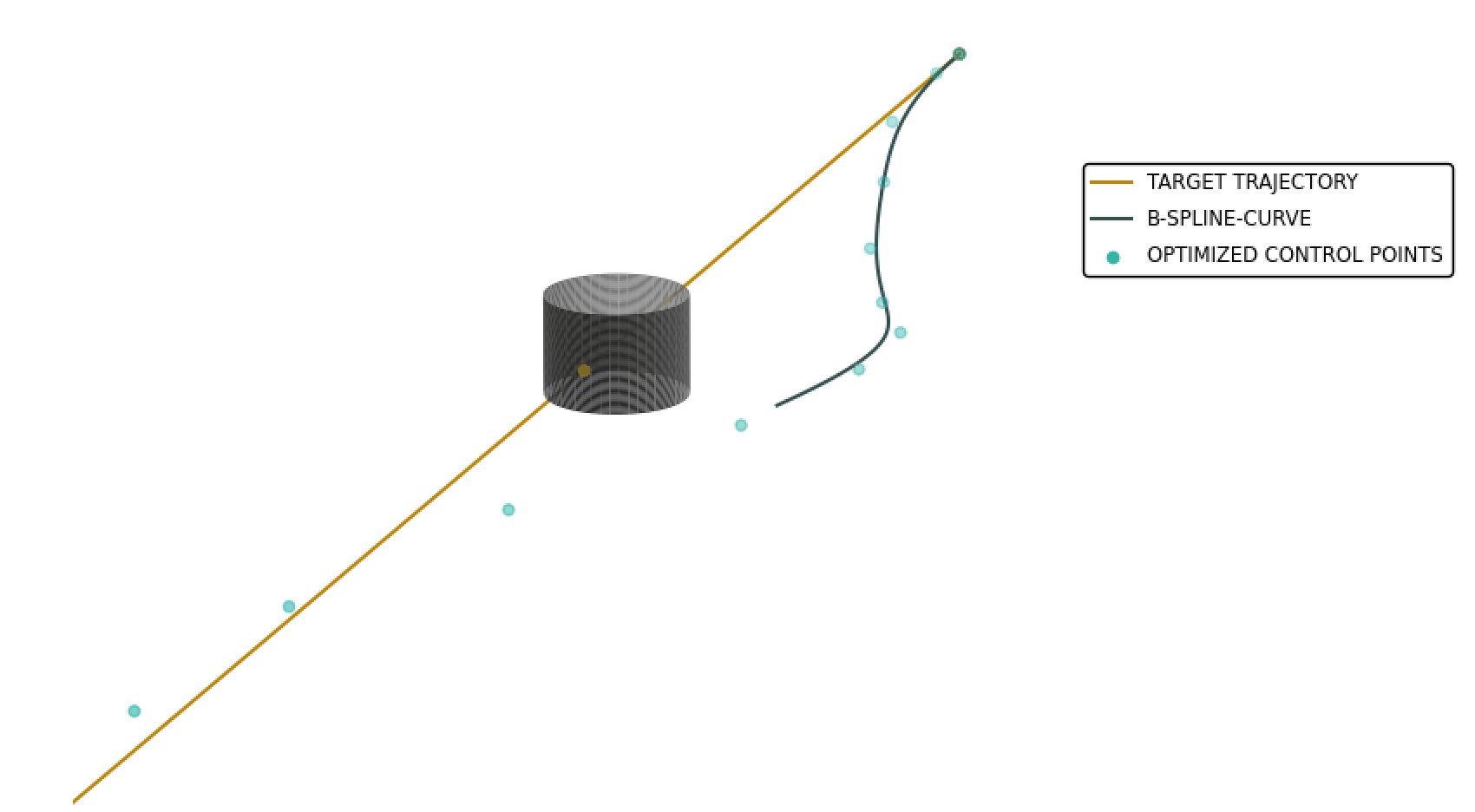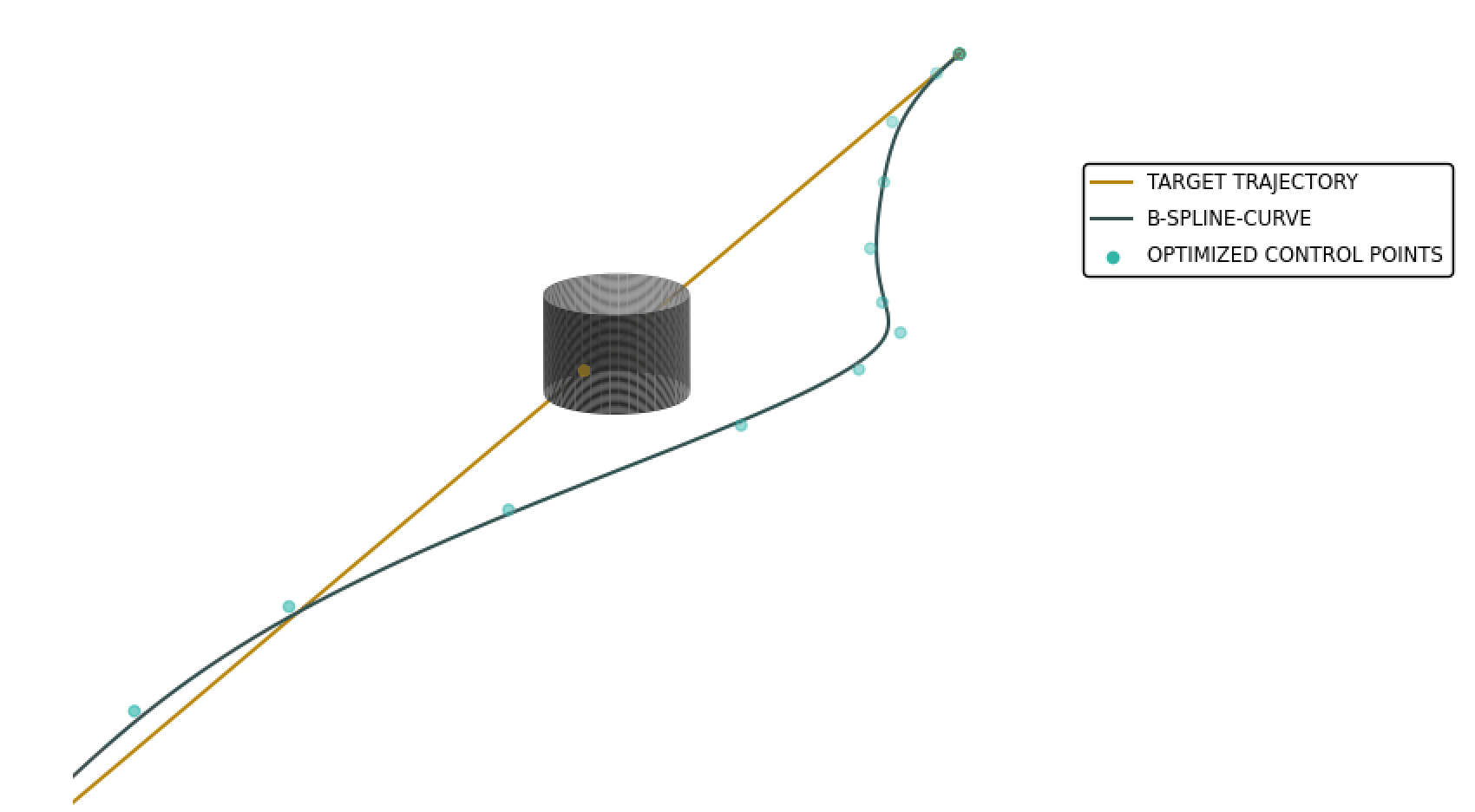
Autonomous vehicles will be an integral part of our environment and will have a significant impact on transportation and other industries. In this context, drones, so-called UAVs will be used for aerial transportation. Due to the high information density, motion planning is a fundamental problem in the autonomous movement of vehicles.
In the future, drones should transport goods or perhaps people in a fast, safe and thus collision-free manner. In doing so, the drone should be able to perform all calculations quickly, accurately and autonomously. Therefore, it makes sense to develop algorithms that meet these requirements.
As part of a bachelor thesis, a method [1] was investigated that uses uniform B-splines to replan a drone’s trajectory in the presence of a potential collision. This method formulates the task of replanning the trajectory as the solution to a non-linear optimization problem.
\begin{align*}
E=\lambda_{ep}(p(t_{ep})-p_{ep})^{2}+\lambda_{ep}(p'(t_{ep})-p’_{ep})^{2} + \lambda_{c} \int_{t_{min}}^{t_{max}}c(p(t))||p'(t)||dt + \sum_{i=2}^{4}\int_{t_{min}}^{t_{max}}\lambda_{q}(p^{(i)}(t))^{2}dt
\end{align*}
With this simplified equation, three cost terms are considered: Endpoint error, collision cost and quadratic derivative cost. With the goal of computing an efficient and collision-free trajectory, an iterative process is used to construct a B-spline curve such that it follows a pre-planned and optimal trajectory. The focus of the analysis was on the selection of the control parameters λep, λc, λq, as well as the number of control points to be optimized and the resulting properties of the optimized trajectory. Using a uniform knot vector, the B-spline is expanded to include control points whose spatial coordinates are determined using nonlinear optimization so that the objective function is minimized. Due to the properties of B-splines, upcoming segments can be locally optimized so that a collision is prevented. The use of a uniform knot vector allows an efficient replanning of the trajectory in real time, which can be performed autonomously by a drone. The following figure shows one result.[1] Vladyslav Usenko, Lukas von Stumberg, Andrej Pangercic, Daniel Cremers, Real-Time Trajectory Replanning for MAVs using Uniform B-splines and a 3D Circular Buffer, Technical University of Munich, 2017, https://arxiv.org/abs/1703.01416.
- Thesis Snapshot: The effect of sea ice seasonality on the two-dimensional energy balance model ‘Klimakoffer’ (Bachelor thesis by Xenia Ibach) May 3, 2022
In a previous snapshot, the two-dimensional energy balance model has been already presented:\begin{align*}
C(\hat{r})\frac{\partial T(\hat{r},t)}{\partial t} +A+BT(\hat{r},t)= \nabla\cdot(D(\hat{r})\nabla T(\hat{r},t)) + QS(\hat{r},t)(1-a(\hat{r}))
\end{align*}
The model is based on the assumption of a static surface distribution of the surface types land, ocean, sea ice and snow. However, climate change at an increasing rate is also affecting surface types seasonally as well as permanently over the years. Melting ice and snow masses worldwide are a consequence of this, affecting not only snow and sea ice distribution, but also that of oceans and land surfaces through rising sea ice levels.
Therefore, for more accurate climate modeling with this EBM, it is interesting to modify the model with respect to a time-dependent surface distribution. This modification directly affects the model parameters albedo, solar forcing, and heat capacity, requiring the following reformulation of the model:
\begin{align*}
C(\hat{r},t)\frac{\partial T(\hat{r},t)}{\partial t} +A+BT(\hat{r},t)= \nabla\cdot(D(\hat{r})\nabla T(\hat{r},t)) + QS(\hat{r},t)(1-a(\hat{r},t))
\end{align*}
As part of a bachelor’s thesis, two options were presented for introducing a seasonal sea ice distribution into the EBM by using and modifying simulations from the ‘Klimakoffer‘. Similar approaches are also conceivable for the other surface types.
One possibility is to process documented measurements of sea ice distribution, available for example from institutions such as the NSIDC (National Snow and Sea Ice Data Center) or NASA, so that a monthly change in sea ice distribution at the edge of the sea ice extent at the two poles can be mapped using a specially developed algorithm.
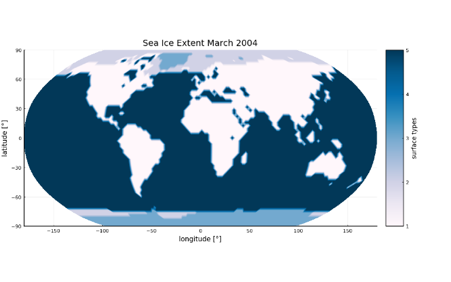
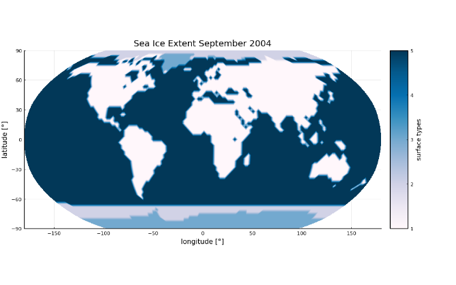
A second option is to directly read in satellite images and categorize the color values of the image’s pixels and map them to the surface types required in the EBM. Here, as an example, a satellite image of the Blue Marble series from 2004 of NASA was read in and categorized on the basis of the color values to the different surface types.
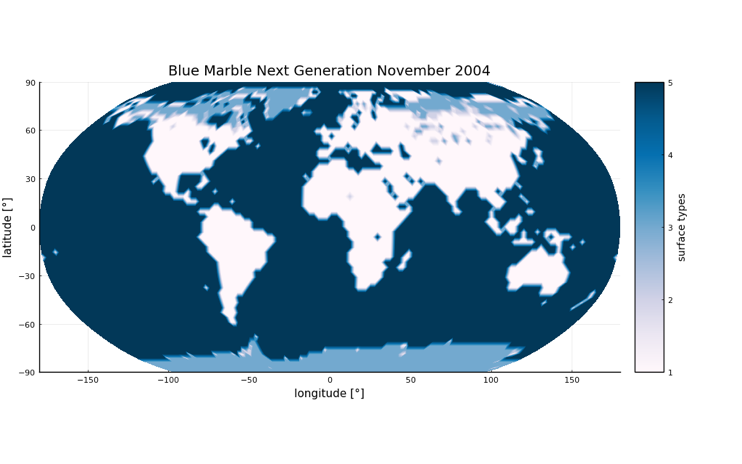
[1] North, G.R.; Mengel, J.G.; Short, D.A. (1983). Simple Energy Balance Model Resolving the Seasons and the Continents’ Application to the Astronomical Theory of the Ice Ages. Journal of Geophysical Research.
[2] Zhuang, K.; North, G.R.; Stevens, Mark J. (2017). A NetCDF version of the two-dimensional energy balance model based on the full multigrid algorithm. SoftwareX.
[3] EOS Project Science Office at NASA Goddard Space Flight Center, Blue Marble Next Generation, 2004, https://visibleearth.nasa.gov/collection/1484/blue-marble. - Start of new Research Project: DFG funded Research Unit “SNUBIC: Structure-Preserving Numerical Methods for Bulk- and Interface Coupling of Heterogeneous Models” (2022 – 2026) April 15, 2022
Funded by the German Research Foundation under the grant number DFG-FOR5409 to investigate the modeling and simulation of coupled systems described by partial differential equations (PDEs).
Please visit the research unit webpage for all the details: SNUBIC.
- Start of new Research Project: Klaus-Tschira-Stiftung funded Project “HiFiLab: A High-Fidelity Laboratory for the Simulation of Celestial Bodies with their Space Environment” (2022 – 2025) April 1, 2022
In this project, we focus on generating a novel computational simulation framework to describe the interaction of plasma with celestial bodies. Understanding the interaction of celestial bodies with their space environment is very important, as it often reveals information about their inner structure and the existence/composition of their atmospheres. Of fundamental importance is the question about liquid water under the icy surface of some moons of the solar system, as water is considered to be one of the essential ingredients for life as we know it.In the last years, we have successfully designed a high-order accurate 3D unstructured discontinuous Galerkin (DG) open source solver with fully parallel adaptive mesh refinement for single-fluid magnetohydrodynamics. DG methods are famous for their high accuracy, their high flexibility and extreme parallel scaling capabilities and are thus perfectly suited for complex plasma interaction simulations. We plan a major step forward regarding the physical modeling fidelity of our computational plasma framework, by extending our high-order DG solver to multi-ion MHD models that account for the interaction of electrons, ions, and neutrals. We will further apply the resulting novel computational plasma framework to simulate the Jovian moon Europa and compare our results with data taken by space missions during flybys of the moon and observations from the Hubble Space Telescope to gain insight and better understanding of the complex plasma interactions.
- Snapshot: A high order detonation diffraction simulation with reactive Euler equations March 23, 2022
We show a detonation diffraction simulation with multiple obstacles in a reflective box using reactive multicomponent Euler equations with Trixi.jl. These kind of detonation waves may result in pressure and density drops close to zero which is numerically difficult not only but especially for high order schemes.

In this simulation we use a reacting model which consists of one reaction and two species. This example has been calculated using the high order DG-FV blending method in Trixi.jl with a HOHQMesh generated mesh whereas the chemical network is solved with KROME.
(Note: Not all of these features are currently available in the main code of Trixi.jl.)
- New paper submitted: On the Theoretical Foundation of Overset Grid Methods for Hyperbolic Problems II: Entropy Bounded Formulations for Nonlinear Conservation Laws March 22, 2022
We derive entropy conserving and entropy dissipative overlapping domain formulations for systems of nonlinear hyperbolic equations in conservation form, such as would be approximated by overset mesh methods. The entropy conserving formulation imposes two-way coupling at the artificial interface boundaries through nonlinear penalty functions that vanish when the solutions coincide. The penalty functions are expressed in terms of entropy conserving fluxes originally introduced for finite volume schemes. Entropy dissipation and additional coupling in the overlap region are added through the use of linear penalties.
- New paper submitted: On the entropy projection and the robustness of high order entropy stable discontinuous Galerkin schemes for under-resolved flows March 22, 2022
High order entropy stable schemes provide improved robustness for computational simulations of fluid flows. However, additional stabilization and positivity preserving limiting can still be required for variable-density flows with under-resolved features. We demonstrate numerically that entropy stable DG methods which incorporate an “entropy projection” are less likely to require additional limiting to retain positivity for certain types of flows. We conclude by investigating potential explanations for this observed improvement in robustness.
- New paper submitted: Entropy-Stable Gauss Collocation Methods for Ideal Magneto-Hydrodynamics March 14, 2022
In this paper, we present an entropy-stable Gauss collocation discontinuous Galerkin (DG) method on 3D curvilinear meshes for the GLM-MHD equations: the single-fluid magneto-hydrodynamics (MHD) equations with a generalized Lagrange multiplier (GLM) divergence cleaning mechanism. For the continuous entropy analysis to hold and to ensure Galilean invariance in the divergence cleaning technique, the GLM-MHD system requires the use of non-conservative terms.
Traditionally, entropy-stable DG discretizations have used a collocated nodal variant of the DG method, also known as the discontinuous Galerkin spectral element method (DGSEM) on Legendre-Gauss-Lobatto (LGL) points. Recently, Chan et al. (“Efficient Entropy Stable Gauss Collocation Methods”. SIAM -2019) presented an entropy-stable DGSEM scheme that uses Legendre-Gauss points (instead of LGL points) for conservation laws. Our main contribution is to extend the discretization technique of Chan et al. to the non-conservative GLM-MHD system.
We provide a numerical verification of the entropy behavior and convergence properties of our novel scheme on 3D curvilinear meshes. Moreover, we test the robustness and accuracy of our scheme with a magneto-hydrodynamic Kelvin-Helmholtz instability problem. The numerical experiments suggest that the entropy-stable DGSEM on Gauss points for the GLM-MHD system is more accurate than the LGL counterpart. - Snapshot: Supersonic turbulence simulations with FLUXO February 25, 2022
We show a supersonic turbulence simulation in a periodic box fueled by perpetual kinetic energy injection on the largest three modes. Such setups are subject of active research in astrophysics and are believed to play an important role in the dynamics of galactic clouds and star formation, e.g., [1,2,3]. An initially uniform density distribution (left plot in the video) is gradually driven to a turbulent state till an average velocity of Mach 3.5 is reached (about t=0.19). Locally, speeds can spike above Mach 35 (bottom right plot in the video). The simulation was computed on FLUXO (https://github.com/project-fluxo/fluxo) with a robust invariant domain preserving Discontinuous Galerkin scheme (DG) [4] solving the compressible, quasi-isothermal ($\gamma =1.001$) Euler equations on a uniform grid with $128^3$ degrees-of-freedom.
Smooth blending with a monotone finite volume scheme stabilizes the high-order DG at strongly shocked regions (filaments of high density concentration) displayed by the blending parameter plot (top right in the video). Blue encodes regions of 100% high order DG while red dots indicate focused blending with FV. Hypersonic turbulence regimes are very challenging for any numerical scheme considering the stark gradients in density, bubbles of near-vacuum and the extremely high speeds involved in such simulations.
[1] https://academic.oup.com/mnras/article/436/2/1245/1126116
[2] https://adsabs.harvard.edu/full/1981MNRAS.194..809L]
[3] https://academic.oup.com/mnras/article/480/3/3916/5060766
[4] Rueda-Ramírez, A. M., Pazner, W., & Gassner, G. J. (2022). Subcell limiting strategies for discontinuous Galerkin spectral element methods. arXiv preprint arXiv:2202.00576. - Snapshot: Hypersonic astrophysical jet (Mach~2000) simulation using a hybrid DG/FV solver January 31, 2022
Simulation of a hypersonic astrophysical jet with Mach=2156.91 moving through a medium at rest.
The simulation was performed on a 256 × 256 quadrilateral grid with a nodal fourth-order entropy-stable Discontinuous Galerkin (DG) scheme. Local bounds on the density and specific entropy are imposed by blending the DG scheme locally (at the node level) with a second-order Finite Volume (FV) method. Both the DG and the FV methods use the Harten-Lax-van Leer-Einfeldt (HLLE) Riemann solver.
The simulation results were obtained with the open-source code FLUXO (https://github.com/project-fluxo/fluxo).
The numerical methods used to perform the simulation are described in our preprint:
Rueda-Ramírez, A. M., Pazner, W., Gassner, G.J. (2022). Subcell Limiting Strategies for Discontinuous Galerkin Spectral Element Methods. Submitted. https://arxiv.org/abs/2202.00576. - New paper submitted: Subcell limiting strategies for discontinuous Galerkin spectral element methods January 31, 2022
We present a general family of subcell limiting strategies to construct robust high-order accurate nodal discontinuous Galerkin (DG) schemes. The main strategy is to construct compatible low order finite volume (FV) type discretizations that allow for convex blending with the high-order variant with the goal of guaranteeing additional properties, such as bounds on physical quantities and/or guaranteed entropy dissipation. For an implementation of this main strategy, four main ingredients are identified that may be combined in a flexible manner: (i) a nodal high-order DG method on Legendre-Gauss-Lobatto nodes, (ii) a compatible robust subcell FV scheme, (iii) a convex combination strategy for the two schemes, which can be element-wise or subcell-wise, and (iv) a strategy to compute the convex blending factors, which can be either based on heuristic troubled-cell indicators, or using ideas from flux-corrected transport methods.
By carefully designing the metric terms of the subcell FV method, the resulting methods can be used on unstructured curvilinear meshes, are locally conservative, can handle strong shocks efficiently while directly guaranteeing physical bounds on quantities such as density, pressure or entropy. We further show that it is possible to choose the four ingredients to recover existing methods such as a provably entropy dissipative subcell shock-capturing approach or a sparse invariant domain preserving approach.
We test the versatility of the presented strategies and mix and match the four ingredients to solve challenging simulation setups, such as the KPP problem (a hyperbolic conservation law with non-convex flux function), turbulent and hypersonic Euler simulations, and MHD problems featuring shocks and turbulence. - New Open Position: PostDoc in Scientific Computing January 27, 2022
The Numerical Simulation group of Professor Gassner invites applications for a 2 year (possibility for extensions afterwards available) postdoc position in scientific computing (pay grade 100% TVL-13).
Deadline for applications is 28.2.2022.
For details, please have a look at the job ad:
German version (click here)
English version (click here)For questions, please directly contact Professor Gassner via Email (ggassner@uni-koeln.de).
- New paper submitted: A Discontinuous Galerkin Solver in the FLASH Multi-Physics Framework December 22, 2021
In this paper, we present a discontinuous Galerkin solver based on previous work by Markert et al. (2021) for magneto-hydrodynamics in form of a new fluid solver module integrated into the established and well-known multi-physics simulation code FLASH. Our goal is to enable future research on the capabilities and potential advantages of discontinuous Galerkin methods for complex multi-physics simulations in astrophysical settings. We give specific details and adjustments of our implementation within the FLASH framework and present extensive validations and test cases, specifically its interaction with several other physics modules such as (self-)gravity and radiative transfer. We conclude that the new DG solver module in FLASH is ready for use in astrophysics simulations and thus ready for assessments and investigations.
- New paper submitted: Efficient implementation of modern entropy stable and kinetic energy preserving discontinuous Galerkin methods for conservation laws December 22, 2021
Many modern discontinuous Galerkin (DG) methods for conservation laws make use of summation by parts operators and flux differencing to achieve kinetic energy preservation or entropy stability. While these techniques increase the robustness of DG methods significantly, they are also computationally more demanding than standard weak form nodal DG methods. We present several implementation techniques to improve the efficiency of flux differencing DG methods that use tensor product quadrilateral or hexahedral elements, in 2D or 3D respectively. Focus is mostly given to CPUs and DG methods for the compressible Euler equations, although these techniques are generally also useful for GPU computing and other physical systems including the compressible Navier-Stokes and magnetohydrodynamics equations. We present results using two open source codes, Trixi.jl written in Julia and FLUXO written in Fortran, to demonstrate that our proposed implementation techniques are applicable to different code bases and programming languages.
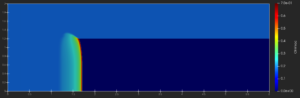
- Snapshot: Immersed Boundary Discontinuous Galerkin Simulation of Flow Past a Cylinder at Re=100 November 30, 2021
Simulation of the viscous flow past a cylinder with a discontinuous Galerkin spectral element method on a hierarchical Cartesian mesh with adaptive mesh refinement (AMR). The polynomial degree is N = 3 and the mesh uses five refinement levels. The cylinder boundary is imposed with an immersed boundary method (IBM) based on volume penalization [1], which adds a source term to the compressible Navier-Stokes equations,
$$
\partial_t \mathbf{u} + \nabla \cdot \vec{\mathbf{f}} (\mathbf{u},\nabla \mathbf{u}) = \underbrace{\beta (\mathbf{u}_s – \mathbf{u})}_{\text{IBM source}},
$$
where $\mathbf{u}$ is the vector of conservative quantities, $\vec{\mathbf{f}}$ is the Navier-Stokes flux, $\beta$ is the penalty parameter, and $\mathbf{u}_s$ is an imposed state. For this simulation, $\mathbf{u}_s$ mimics an isothermal no-slip wall boundary condition.The simulation was obtained with the open-source code FLUXO (https://github.com/project-fluxo/fluxo).
References
[1] Kou, J., Joshi, S., Hurtado-de-Mendoza, A., Puri, K., Hirsch, C., & Ferrer, E. (2022). Immersed boundary method for high-order flux reconstruction based on volume penalization. Journal of Computational Physics, 448, 110721. - New paper published: On the theoretical foundation of overset grid methods for hyperbolic problems: Well-posedness and conservation October 27, 2021
We use the energy method to study the well-posedness of initial-boundary value problems approximated by overset mesh methods in one and two space dimensions for linear constant-coefficient hyperbolic systems. We show that in one space dimension, for both scalar equations and systems of equations, the problem where one domain partially oversets another is well-posed when characteristic coupling conditions are used. If a system cannot be diagonalized, as is usually the case in multiple space dimensions, then the energy method does not give proper bounds in terms of initial and boundary data. For those problems, we propose a novel penalty approach. We show, by using a global energy that accounts for the energy in the overlap region of the domains, that under well-defined conditions on the coupling matrices the penalized overset domain problems are energy bounded, conservative, well-posed and have solutions equivalent to the original single domain problem.
Published in Journal of Computational Physics (ScienceDirect)
- Snapshot: Simulation of a stiff multi-species reacting flow October 19, 2021
Simulation of an asymmetric two-dimensional stiff multi-species reacting flow for the compressible Euler equations. The computation domain
[0,6]x[0,2]of this detonation problem is split into three zones. Zone A[0,0.5]x[0,2]as well as zone B(0.5,6]x[1.2,2]is filled with burnt gas, namelyO2,OHandH2O. The last zone C(0.5,6]x[0,1.2)contains unburnt gas, namelyH2andO2.The reacting model consists of two reactions
H2+O2->2OH,2OH+H2->2H2Oand five speciesH2,O2,OH,H2O,N2whereas reaction 1 has a smaller ignition temperature as well as a much faster chemical rate than reaction 2. SpeciesN2acts as a dilute catalyst here.This example has been calculated using Trixi.jl with a P4est mesh using
3072x1024=3.145.728elements, Dirichlet boundary conditions in x-direction as well as solid wall boundaries in y-direction. The final time is T = 0.1. The convection part is solved with FV whereas the chemical network is solved with KROME. (Note: Not all of these features are currently available in the main code of Trixi.jl.)Pressure distribution at final time T=0.1:

Temperature distribution at final time T=0.1:

- Snapshot: Numerical simulations of earth’s climate September 30, 2021
Earth’s climate is changing due to human activity. Therefore, the ability to predict future climate change is of utmost importance if we want to reduce the human interference with the climate system (climate change mitigation) and our vulnerability to the harmful effects of climate change (climate change adaptation).
It is possible to model the time-dependent local temperatures on the globe using a simple two-dimensional energy balance model [1,2],
$$ C(\vec{x}) \frac{\partial T}{\partial t} + A + BT = \nabla \cdot \left( D(\vec{x}) \nabla T \right) + Q S(\vec{x},t) (1-a(\vec{x})), $$
where $T$ is the local temperature; $C(\vec{x})$ is the local heat capacity for a column of air on land, water or ice; the term $A+BT$ models the outgoing long-wave radiation, where $A$ depends on the amount of green-house gases in the atmosphere and $B$ models several feedback effects; $D$ is a latitude-dependent diffusion coefficient; and the last term includes the heat input in the system, where $Q$ is the solar radiation at earth’s position in the solar system, $S$ is the seasonal and latitudinal distribution of insolation, which depends on orbital parameters, such as the eccentricity of earth’s orbit, and the precession and tilt of earth’s rotation axis, and $a(\vec{x})$ is the local albedo, which measures the reflection of solar radiation and depends on the surface cover.We developed a julia code that implements the EBM model on the sphere surface and used it to describe the mean temperatures on the globe assuming a constant atmospheric CO$_2$ concentration (of year 1950). The results are presented in the animation.
[1] North, G.R.; Mengel, J.G.; Short, D.A. (1983). Simple Energy Balance Model Resolving the Seasons and the Continents’ Application to the Astronomical Theory of the Ice Ages. Journal of Geophysical Research.
[2] Zhuang, K.; North, G.R.; Stevens, Mark J. (2017). A NetCDF version of the two-dimensional energy balance model based on the full multigrid algorithm. SoftwareX. - Snapshot: Simulation of a colliding flow setup with DGSEM August 15, 2021Simulation of a colliding flow setup with DGSEM (polynomial degree 3,compatible sub-cell LGL type FV for shock capturing) of the compressibleEuler equations, where at x = +/- 64 inflow boundary conditions withMach number Ma = 70 is set (with periodic boundary conditions in y
- JuliaCon 2021: Adaptive and extendable numerical simulations with Trixi.jl August 9, 2021
Trixi.jl is a numerical simulation framework for adaptive, high-order discretizations of conservation laws. It has a modular architecture that allows users to easily extend its functionality and was designed to be useful to experienced researchers and new users alike. In this talk, we give an overview of Trixi’s current features, present a typical workflow for creating and running a simulation, and show how to add new capabilities for your own research projects.
This talk was given on July 30th, 2021 by Michael Schlottke-Lakemper and Hendrik Ranocha as part of JuliaCon 2021.
Talk on YouTube: https://www.youtube.com/watch?v=hoViWRAhCBE
Repository: https://github.com/trixi-framework/talk-2021-juliacon
Conference agenda entry: https://live.juliacon.org/talk/VAGFD7 - New paper published: An entropy stable nodal discontinuous Galerkin method for the resistive MHD equations. Part II: Subcell finite volume shock capturing August 3, 2021
The second paper of this series presents two robust entropy stable shock-capturing methods for discontinuous Galerkin spectral element (DGSEM) discretizations of the compressible magneto-hydrodynamics (MHD) equations. Specifically, we use the resistive GLM-MHD equations, which include a divergence cleaning mechanism that is based on a generalized Lagrange multiplier (GLM). For the continuous entropy analysis to hold, and due to the divergence-free constraint on the magnetic field, the GLM-MHD system requires the use of non-conservative terms, which need special treatment.
Hennemann et al. (2020) [25] recently presented an entropy stable shock-capturing strategy for DGSEM discretizations of the Euler equations that blends the DGSEM scheme with a subcell first-order finite volume (FV) method. Our first contribution is the extension of the method of Hennemann et al. to systems with non-conservative terms, such as the GLM-MHD equations. In our approach, the advective and non-conservative terms of the equations are discretized with a hybrid FV/DGSEM scheme, whereas the visco-resistive terms are discretized only with the high-order DGSEM method. We prove that the extended method is semi-discretely entropy stable on three-dimensional unstructured curvilinear meshes. Our second contribution is the derivation and analysis of a second entropy stable shock-capturing method that provides enhanced resolution by using a subcell reconstruction procedure that is carefully built to ensure entropy stability.
We provide a numerical verification of the properties of the hybrid FV/DGSEM schemes on curvilinear meshes and show their robustness and accuracy with common benchmark cases, such as the Orszag-Tang vortex and the GEM (Geospace Environmental Modeling) reconnection challenge. Finally, we simulate a space physics application: the interaction of Jupiter’s magnetic field with the plasma torus generated by the moon Io.
Published in Journal of Computational Physics (ScienceDirect)
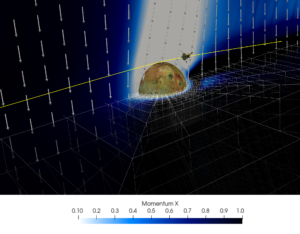
- Snapshot: Interaction of Jupiter’s moon Io with the Jovian magnetosphere July 31, 2021
Io is the most volcanically active body of the solar system. Furthermore, it is embedded in Jupiter’s magnetic field, the largest and most powerful planetary magnetosphere of the solar system. Due to its strong volcanic activity, Io expels ions and neutrals, which are in turn ionized by ultraviolet and electron impact ionization, forming a plasma torus around Jupiter [1,2]. As Io moves inside the plasma torus, elastic collisions of ions and neutrals inside its atmosphere generate a magnetospheric disturbance that propagates away from Io along the background magnetic field lines at the Alfvén wave speed. This phenomenon creates a pair of Alfvén current tubes that are commonly called Alfvén wings, which have been observed by several flybys [1].
The figure shows the momentum (non-dimensional) and magnetic field of the plasma that surrounds Io, obtained with the magneto-hydrodynamic (MHD) plasma model of FLUXO*. The Alfvén wings can be observed as disturbances of both the background magnetic and momentum fields. In yellow is the trajectory of the I31 flyby of the Galileo spacecraft, which visited Io in 2001 [1]. The Galileo spacecraft is also depicted (not to scale). A 3D model of the moon’s surface developed by NASA [3] was superposed on the simulation results.
*FLUXO (www.github.com/project-fluxo/fluxo) is an MPI parallel high-order Discontinuous Galerkin code, which supports unstructured curvilinear hexahedral grids, and is able to perform Adaptive Mesh Refinement (AMR).
[1] M. Kivelson, K. Khurana, C. Russell, R. Walker, S. Joy, J. Mafi, GALILEO ORBITER AT JUPITER CALIBRATED MAG HIGH RES V1.0, GO-J-MAG-3-RDR-HIGHRES-V1.0, Technical Report, NASA Planetary Data System, 1997.
[2] J. Saur, F. M. Neubauer, J. E. P. Connerney, Plasma interaction of Io with its plasma torus, 2004.
[3] https://solarsystem.nasa.gov/resources/2379/io-3d-model/ - Talk on 2021-07-02: On Wave Propagation Characteristics, Upwind SBP Properties and Energy Stability of DG Viscous Flux Discretizations June 28, 2021
Speaker: Dr. Sigrun Ortleb, University of Kassel, Germany
Date & time: Friday, 2nd July 2021, 10 am (CEST)
Venue: Please request the Zoom meeting link from Michael Schlottke-LakemperAbstract:
Regarding accuracy and stability of numerical schemes for computational fluid dynamics, the investigation of diffusion/dispersion errors depending on the wave number is of utmost importance. Especially for high order methods, a desired small numerical dissipation competes with robustness and thus has to be carefully analyzed. This wave propagation analysis is often based on pure advection problems. In the literature, various approaches to discretize diffusion terms within a DG scheme have been introduced since the discretization of higher order spatial derivatives within the DG framework is less natural than in case of first order derivatives. In this talk, we will address significant differences in the disspation/dispersion properties for linear advection-diffusion, depending on the specific DG viscous flux discretization which is employed. In addition, results on energy stability of DG viscous flux formulations are dealt with and we show how to formulate the well-known LDG and BR1 fluxes in terms of global upwind SBP operators which complements the derivation and analysis regarding element level SBP properties of the DG scheme. - Snapshot: Evolution of a magnetized torus differentially rotating around a static point mass June 24, 2021
Evolution of a magnetized torus differentially rotating around a static point mass. [1] The torus gradually forms into an accretion disk with expanding filaments into the surrounding space due to magneto-rotational instabilities similar to the rich structure of the corona of our sun. The simulation was done with a new Discontinuous-Galerkin based MHD solver [2] in FLASH [3]. Fig. 1 and Fig. 2 show the log. scale density cross section in the x-y and x-z plane. Fig 3 highlights the rich structure of the magnetic field (white stream lines) overlayed on top of the log. scale magnetic pressure in the x-z plane.
[1] Machida, Mami, Mitsuru R. Hayashi, and R. Matsumoto.
“Global simulations of differentially rotating magnetized disks:
Formation of low-beta filaments and structured coronae.”
The Astrophysical Journal Letters 532.1 (2000): L67.
[2] Markert et al. “A Discontinuous Galerkin Method with Sub‑Cell Adaptive Shock Capturing for
FLASH” (in preparation)
[3] http://flash.uchicago.edu/ - Snapshot: Gingerbread man simulation with unstructured quadrilateral elements May 25, 2021
Here we are simulating a gingerbread man, whereby the gingerbread man itself has
861unstructured quadrilateral elements. For the run parameters, we usedpolydeg = 10with the compressible Euler equations and the manufactured (convergence test) solution. The visualization is done onnvisnodes=12uniform points in each direction, on each element.
We thank Prof. Dr. Andrew Winters (https://liu.se/en/employee/andwi94) for providing this video/simulation.
- Talk on 2021-05-21: On a linear stability issue of split form schemes for compressible flows May 19, 2021
Speaker: Dr. Vikram Singh, Max-Planck-Institute for Meteorology
Date & time: Friday, 21st May 2021, 10 am (CEST)
Meeting link: Please request via email from Michael Schlottke-LakemperAbstract:
Split form schemes for Euler and Navier-Stokes equations are useful for computation of turbulent flows due to their better robustness. This is because they satisfy additional conservation properties of the governing equations like kinetic energy preservation leading to a reduction in aliasing errors at high orders. Recently, linear stability issues have been pointed out for these schemes for a density wave problem and we investigate this behaviour for some standard split forms. By deriving linearized equations of split form schemes, we show that most existing schemes do not satisfy a perturbation energy equation that holds at the continuous level. A simple modification to the energy flux of some existing schemes is shown to yield a scheme that is consistent with the energy perturbation equation. Numerical tests are given using a discontinuous Galerkin method to demonstrate these results.Note: This meeting will be recorded.
- New paper submitted: On the Theoretical Foundation of Overset Grid Methods for Hyperbolic Problems: Well-Posedness and Conservation May 12, 2021
We use the energy method to study the well-posedness of initial-boundary value problems approximated by overset mesh methods in one and two space dimensions for linear constant-coefficient hyperbolic systems. We show that in one space dimension, for both scalar equations and systems of equations, the problem where one domain partially oversets another is well-posed when characteristic coupling conditions are used. If a system cannot be diagonalized, as is ususally the case in multiple space dimensions, then the energy method does not give proper bounds in terms of initial and boundary data. For those problems, we propose a novel penalty approach. We show, by using a global energy that accounts for the energy in the overlap region of the domains, that under well-defined conditions on the coupling matrices the penalized overset domain problems are energy bounded, conservative, well-posed and have solutions equivalent to the original single domain problem.
Preprint available at: https://arxiv.org/abs/2105.04664
- Talk on 2021-05-10: A two-dimensional stabilized discontinuous Galerkin method on curvilinear embedded boundary grids May 8, 2021
Speaker: Dr. Andrew Giuliani, New York University
Date & time: Monday, 10th May 2021, 4pm (CEST)/10am (EDT)
Meeting link: Please request via email from Michael Schlottke-LakemperAbstract:
In this talk, we present a state redistribution method for high order discontinuous Galerkin methods on curvilinear embedded boundary grids. State redistribution relaxes the overly restrictive CFL condition that results from arbitrarily small cut cells when explicit time steppers are used. Thus, the scheme can take time steps that are proportional to the size of cells in the background grid. The discontinuous Galerkin scheme is stabilized by postprocessing the numerical solution after each stage or step of an explicit time stepping method. The advantage of this approach is that it uses only basic mesh information that is already available in many cut cell codes and does not require complex geometric manipulations. We prove that state redistribution is conservative and p-exact. Finally, we solve a number of test problems that demonstrate the encouraging potential of this technique for applications on curvilinear embedded geometries. Numerical experiments reveal that our scheme converges with order $p+1$ in $L_1$ and between $p$ and $p+1$ in $L_\infty$. - New paper published: Stability of Discontinuous Galerkin Spectral Element Schemes for Wave Propagation when the Coefficient Matrices have Jumps May 4, 2021
Abstract:
We use the behavior of the L2 norm of the solutions of linear hyperbolic equations with discontinuous coefficient matrices as a surrogate to infer stability of discontinuous Galerkin spectral element methods (DGSEM). Although the L2 norm is not bounded by the initial data for homogeneous and dissipative boundary conditions for such systems, the L2 norm is easier to work with than a norm that discounts growth due to the discontinuities. We show that the DGSEM with an upwind numerical flux that satisfies the Rankine-Hugoniot (or conservation) condition has the same energy bound as the partial differential equation does in the L2 norm, plus an added dissipation that depends on how much the approximate solution fails to satisfy the Rankine-Hugoniot jump.
Accepted in Journal of Scientific Computing.
arXiv link: https://arxiv.org/abs/2011.11746
- Snapshot: Astrophysical colliding flow simulation run by a novel Discontinuous Galerkin/Finite Volume (DGFV) blending scheme in FLASH April 29, 2021
Simulation of an astrophysical colliding flow [1] run by a novel Discontinuous Galerkin/Finite Volume (DGFV) blending scheme [2] which has been implemented in the FLASH code [3].
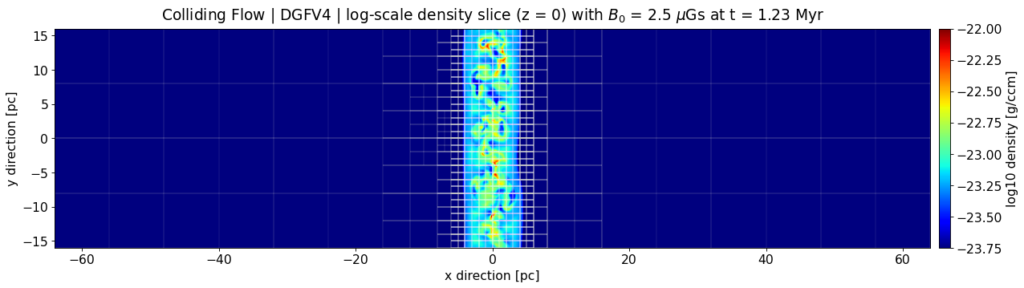
The code has following capabilities:
- fourth-order accurate ideal magneto-hydrodynamics with hyperbolic divergence cleaning [4]
- octree-based adaptive mesh refinement
- distributive computing and load balancing
- multi-species fluid dynamics (N_species > 10)
- turbulent driving
- octree-based Poisson solver for self-gravity [5]
- octree-based radiation physics [6]
- external gravitional fields
- sink particles [7]
- chemical reaction networks [8]
[1] Weis, Micheal et al. “The Virial Balance of CO-Substructures in Colliding Magnetised Flows” (in preparation)
[2] Markert, Johannes et al. “A Sub-Element Adaptive Shock Capturing Approach for Discontinuous Galerkin Methods” (submitted)
[3] Fryxell, Bruce, et al. “FLASH: An adaptive mesh hydrodynamics code for modeling astrophysical thermonuclear flashes.” The Astrophysical Journal Supplement Series 131.1 (2000): 273.
[4] Markert, Johannes et al. “Flash goes DG” (working title, in preparation)
[5] Wünsch, Richard, et al. “Tree-based solvers for adaptive mesh refinement code FLASH–I: gravity and optical depths.” Monthly Notices of the Royal Astronomical Society 475.3 (2018): 3393-3418.
[6] Wünsch, Richard et al. “Tree-based solvers for adaptive mesh refinement code FLASH – II: radiation transport module TreeRay” (submitted)
[7] Federrath, Christoph, et al. “Modeling collapse and accretion in turbulent gas clouds: implementation and comparison of sink particles in AMR and SPH.” The Astrophysical Journal 713.1 (2010): 269.
[8] Seifried, D., and S. Walch. “Modelling the chemistry of star-forming filaments–I. H2 and CO chemistry.” Monthly Notices of the Royal Astronomical Society: Letters 459.1 (2016): L11-L15. - Snapshot: Simulation of a Kelvin-Helmholtz instability using second order Finite Volume schemes and fourth order Discontinuous Galerkin methods April 1, 2021
We present in-viscid and viscous simulations of a Kelvin-Helmholtz instability using second a order accurate monotoniced-central finite volume (FV) method and a fourth order accurate discontinuous Galerkin (DG) method. The initial condition is given by [1]:
$$\rho (t=0) = \frac{1}{2}
+ \frac{3}{4} B,
~~~~~~~~~
p (t=0) = 1,~~~~~~~~~~
$$$$
v_1 (t=0) = \frac{1}{2} \left( B-1 \right),
~~~~~~~
v_2 (t=0) = \frac{1}{10} \sin(2 \pi x),
$$with $$B=\tanh \left( 15 y + 7.5 \right) – \tanh(15y-7.5).$$
We first present the FV results at end time $t=3.7$, which are computed using a monotoniced-central second order discretization of the Euler equations of gas dynamics on uniform grids.
The next results use a fourth order DG discretization of the Navier-Stokes equations on uniform grids using $Re=320.000$ at end time $t=3.7$. The highest resolution (4096² DOFs) is a direct numerical simulation (DNS) of the problem, where all scales are resolved.
It is remarkable that the numerical dissipation of the second order FV scheme causes the in-viscid simulation with 2048² DOFs to look very similar to the viscous DNS solution at $Re=320.000$.
[1] A.M. Rueda-Ramírez, G.J Gassner (2021). A Subcell Finite Volume Positivity-Preserving Limiter for DGSEM Discretizations of the Euler Equations. https://arxiv.org/pdf/2102.06017.pdf
- Talk on 2021-03-18: A tour of BifurcationKit and some results on mean fields of spiking neurons March 12, 2021
Speaker: Dr. Romain Veltz, INRIA, France
Date: Thursday, 18th March 2021, 10am (CET)
Zoom-Link: Please request via email from Michael Schlottke-LakemperAbstract
In this talk, I will first present the basics of bifurcation theory. Then, I will give a panorama of
BifurcationKit.jl, a Julia package to perform numerical bifurcation analysis of large dimensional equations (PDE, nonlocal equations, etc) possibly on GPUs using Matrix-Free / Sparse Matrix formulations of the problem. Julia programming language gives access to a rich ecosystem (PDE, GPU, AD, cluster…). Notably, numerical bifurcation analysis can be done entirely on GPU as will be shown in an example.BifurcationKitincorporates continuation algorithms (PALC, deflated continuation, …) which can be used to perform fully automatic bifurcation diagram computation of stationary states. I will showcase this with the 2d Bratu problem.Additionally, by leveraging on the above methods, the package can also seek for periodic orbits of Cauchy problems by casting them into an equation of high dimension. It is by now, one of the only software which provides parallel (Standard / Poincaré) shooting methods and finite differences based methods to compute periodic orbits in high dimensions. I will present an application highlighting the ability to fine tune
BifurcationKitto get performance.In a last part, I will describe a mean field model of stochastic spiking neurons described with a 2d measure valued equation. I will present a numerical scheme based on an implicit Finite Volume method. I will then provide some mathematical properties of the mean field concerning well posedness and stationary solutions. Additionally, I will show how
BifurcationKit.jlcan be used to study numerically the model. Finally, I will conclude on open problems, some of which could hopefully be tackled numerically withTrixi.jl. - New proceedings paper submitted: A Subcell Finite Volume Positivity-Preserving Limiter for DGSEM Discretizations of the Euler Equations February 25, 2021
In this paper, we present a positivity-preserving limiter for nodal Discontinuous Galerkin disctretizations of the compressible Euler equations. We use a Legendre-Gauss-Lobatto (LGL) Discontinuous Galerkin Spectral Element Method (DGSEM) and blend it locally with a consistent LGL-subcell Finite Volume (FV) discretization using a hybrid FV/DGSEM scheme that was recently proposed for entropy stable shock capturing. We show that our strategy is able to ensure robust simulations with positive density and pressure when using the standard and the split-form DGSEM. Furthermore, we show the applicability of our FV positivity limiter in extremely under-resolved vortex dominated simulations and in problems with shocks.
Preprint available at: https://arxiv.org/pdf/2102.06017.pdf
- Snapshot: Accuracy of the LGL-subcell FV scheme with and without inner-element reconstruction February 24, 2021
We are interested in the accuracy of the finite volume scheme, on a LGL subcell grid induced by a LGL-DGSEM discretization. For comparison, we look at a Kelvin-Helmholtz-Instability test problem, simulated with 4² LGL nodes per element and 32² elements, i.e. 128² spatial degrees of freedom. The high-order DGSEM uses the entropy-conserving split-form powered by the flux of Chandrashekar in the volume, and the HLLC flux at the element interfaces. Positivity is controlled by adding subcell FV where the positivity is not fulfilled with the amount needed. All FV discretizations use the HLLC flux at the element interfaces and at the subcell interfaces as well.
The first results show the high-order DGSEM result, which is formally 4th order accurate for smooth problems: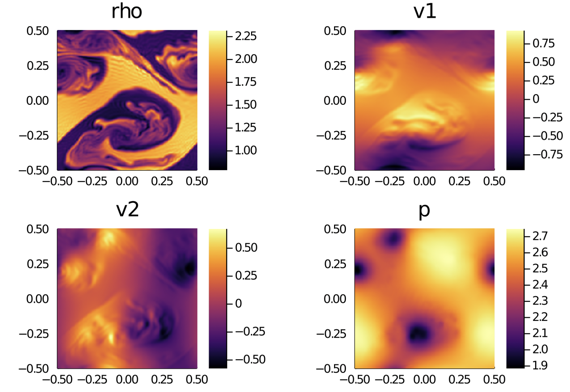
The next result uses a subcell finite volume approximation on the LGL-subcell grid, directly, i.e. without spatial reconstruction (piecewise constant approximation). The result is very dissipative:
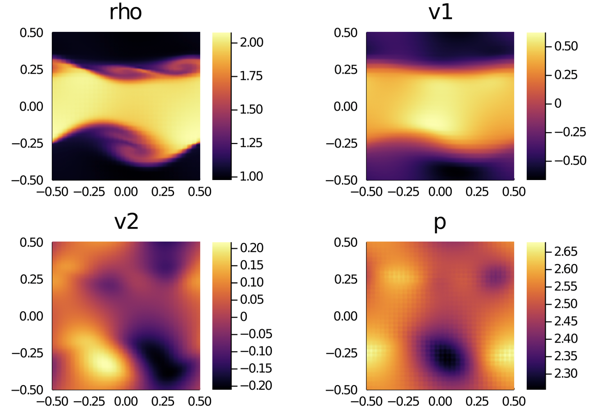
The last results show the improvement when using a piecewise linear reconstruction with monotonized-central slope limiter on the LGL-subcell grid. The reconstruction is inner-element only, as it does not use element neighbor information. Thus, at the very first and very last LGL subcell, no reconstruction is used. Still, the accuracy is recovered nicely by this simple modification of the subcell FV scheme:
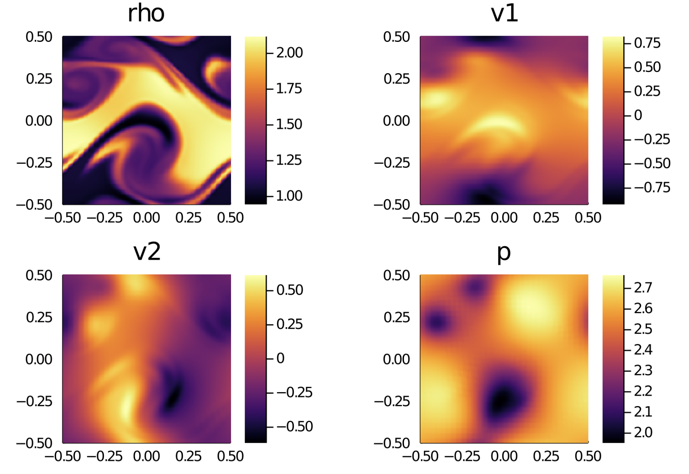
- Snapshot: Single-Node Performance Comparison of Four Different Magnetohydrodynamics Codes January 30, 2021
We compare the runtime performance of four different magnetohydrodynamics codes on a single compute node on the in-house high performance cluster ODIN. A compute node on ODIN consists of 16 cores. We run the ‘3D Alfven wave’ test case up to a fixed simulation time and measure the elapsed wall clock time of each code minus initialization time and input/output operations. For each run the number of cores is successively increased. This allows us to get insights into the scaling behavior (speedup gain wih increasing number of cores) on a single compute node. Furthermore we plot the performance index (PID) over the number of nodes which is a measure of throughput, i.e. how many millions of data points (degrees-of-freedom/DOF) per second are processed by the each code.
The four contestants are:
- Flash [1] with Paramesh 4.0 and the Five-wave Bouchut Finite-Volume solver written in Fortran
- Fluxo [2] an MHD Discontinuous Galerkin Spectral Element code written in Fortran
- Trixi [3] an MHD Discontinuous Galerkin Spectral Element code written in Julia
- Nemo an in-house prototype code providing a 2nd order monotonized-central MHD-FV scheme (MCFV) and a hybrid MHD Discontinuous Galerkin Spectral Element / Finite Volume scheme (DGFV) written in Fortran.
Trixi uses a thread-based parallelization approach while Flash, Fluxo and Nemo
use the standard MPI method. Furthermore, Nemo also provides OpenMP-based
parallelization.[1] https://flash.uchicago.edu/site/
[2] https://github.com/project-fluxo/fluxo
[3] https://github.com/trixi-framework/Trixi.jl - Talk on 2021-01-21: Julia for adaptive high-order multi-physics simulations January 25, 2021
On Wednesday, 27th January 2021, 3:15pm CET, Michael Schlottke-Lakemper will give an online talk on
Julia for adaptive high-order simulations
To obtain the Zoom link, please contact the organizers via the official meeting announcement.
Abstract
Julia has been touted as a programming language especially well-suited for numerical analysis and scientific computing. However, while its prevalence is steadily increasing, it has not yet seen widespread adoption in the computational science or high-performance computing communities. One of the hurdles is a (perceived) lack of real-world examples that show how Julia can be used to conduct numerical simulations and what its advantages and drawbacks are for scientific applications.
To remediate this, in this talk we discuss the development of a purely hyperbolic method for self-gravitating gas dynamics within our Julia-based open source simulation framework Trixi.jl (https://github.com/trixi-framework/Trixi.jl). In this approach, we reformulate the elliptic gravity problem into a hyperbolic diffusion problem, which is solved in pseudotime using the same explicit high-order discontinuous Galerkin method we use for the flow solution. A key benefit is that in the resulting multi-physics simulation problem, we can reuse existing hyperbolic solvers while retaining advanced features such as non-conforming and solution-adaptive meshes.
Next to presenting numerical results, we will critically examine our experience with building a multi-physics simulation framework with Julia. We will discuss its strengths and weaknesses as a programming language for research software engineering, including an assessment of how Julia’s claimed benefits hold up against scientific reality, and give a live demonstration of Julia and Trixi.jl in action.
To make the shown examples reproducible by the audience, the Jupyter notebook used for the live demonstration is available at https://github.com/trixi-framework/talk-2021-julia-adaptive-multi-physics-simulations. It can be either run from a local Julia/Jupyter installation or in the cloud via Binder (without having to install Julia locally). - New paper submitted: An Entropy Stable Nodal Discontinuous Galerkin Method for the resistive MHD Equations. Part II: Subcell Finite Volume Shock Capturing January 4, 2021
The second paper of this series presents two robust entropy stable shock-capturing methods for discontinuous Galerkin spectral element (DGSEM) discretizations of the compressible magneto-hydrodynamics (MHD) equations. Specifically, we use the resistive GLM-MHD equations, which include a divergence cleaning mechanism that is based on a generalized Lagrange multiplier (GLM). For the continuous entropy analysis to hold, and due to the divergence-free constraint on the magnetic field, the GLM-MHD system requires the use of non-conservative terms, which need special treatment.
Hennemann et al. [DOI:10.1016/j.jcp.2020.109935] recently presented an entropy stable shock-capturing strategy for DGSEM discretizations of the Euler equations that blends the DGSEM scheme with a subcell first-order finite volume (FV) method. Our first contribution is the extension of the method of Hennemann et al. to systems with non-conservative terms, such as the GLM-MHD equations. In our approach, the advective and non-conservative terms of the equations are discretized with a hybrid FV/DGSEM scheme, whereas the visco-resistive terms are discretized only with the high-order DGSEM method. We prove that the extended method is entropy stable on three-dimensional unstructured curvilinear meshes. Our second contribution is the derivation and analysis of a second entropy stable shock-capturing method that provides enhanced resolution by using a subcell reconstruction procedure that is carefully built to ensure entropy stability.
We provide a numerical verification of the properties of the hybrid FV/DGSEM schemes on curvilinear meshes and show their robustness and accuracy with common benchmark cases, such as the Orszag-Tang vortex and the GEM reconnection challenge. Finally, we simulate a space physics application: the interaction of Jupiter’s magnetic field with the plasma torus generated by the moon Io.
Preprint available at: arXiv:2012.12040
- Snapshot: Hybrid Discontinuous Galerkin / Finite Volume (DG/FV) simulation of the multicomponent Shock-Bubble Interaction Problem December 24, 2020
Simulation of the Shock-Bubble Interaction Problem with a hybrid entropy-stable DG/FV method and Adaptive Mesh Refinement (AMR) using Trixi (https://github.com/trixi-framework/Tr…).
The simulation uses a multicomponent model and computes the spatial operator as a blend of a first-order subcell FV method and a fourth-order DG scheme on a squared domain.
- New paper published: A Novel Robust Strategy for Discontinuous Galerkin Methods in Computational Fluid Mechanics: Why? When? What? Where? December 15, 2020
In this paper we will review a recent emerging paradigm shift in the construction and analysis of high order Discontinuous Galerkin (DG) methods applied to approximate solutions of hyperbolic or mixed hyperbolic-parabolic partial differential equations (PDEs) in computational physics. There is a long history using DG methods to approximate the solution of PDEs in computational physics with successful applications in linear wave propagation, like those governed by Maxwell’s equations, incompressible and compressible fluid and plasma dynamics governed by the Navier-Stokes and the Magnetohydrodynamics equations, or as a solver for ordinary differential equations (ODEs), e.g., in structural mechanics. The DG method amalgamates ideas from several existing methods such as the Finite Element Galerkin method (FEM) and the Finite Volume method (FVM) and is specifically applied to problems with advection dominated properties, such as fast moving fluids or wave propagation. In the numerics community, DG methods are infamous for being computationally complex and, due to their high order nature, as having issues with robustness, i.e., these methods are sometimes prone to crashing easily. In this article we will focus on efficient nodal versions of the DG scheme and present recent ideas to restore its robustness, its connections to and influence by other sectors of the numerical community, such as the finite difference community, and further discuss this young, but rapidly developing research topic by highlighting the main contributions and a closing discussion about possible next lines of research.
Published in: https://www.frontiersin.org/articles/10.3389/fphy.2020.500690/abstract
Front. Phys. | doi: 10.3389/fphy.2020.500690
- New paper submitted: A Split-Form, Stable CG/DG-SEM for Wave Propagation Modeled by Linear Hyperbolic Systems December 15, 2020
We present a hybrid continuous and discontinuous Galerkin spectral element approximation that leverages the advantages of each approach. The continuous Galerkin approximation is used on interior element faces where the equation properties are continuous. A discontinuous Galerkin approximation is used at physical boundaries and if there is a jump in properties at a face. The approximation uses a split form of the equations and two-point fluxes to ensure stability for unstructured quadrilateral/hexahedral meshes with curved elements. The approximation is also conservative and constant state preserving on such meshes. Spectral accuracy is obtained for all examples, which include wave scattering at a discontinuous medium boundary.
Preprint available at: arXiv:2012.06510
- Snapshot: Hybrid Discontinuous Galerkin / Finite Volume (DG/FV) simulation of the Orszag-Tang vortex November 27, 2020
Simulation of the Orszag-Tang vortex test with a hybrid entropy-stable DG/FV method and Adaptive Mesh Refinement (AMR) using FLUXO (https://github.com/project-fluxo/fluxo).
The simulation uses the GLM-MHD model to control div(B) errors and computes the spatial operator as a blend of a first-order subcell FV method and a fourth-order DG scheme.
The initial grid has 16×16 elements (64² DOFs), and the maximum resolution is achieved with three refinement levels (equivalent to 512² DOFs).
- New paper submitted: Stability of Discontinuous Galerkin Spectral Element Schemes for Wave Propagation when the Coefficient Matrices have Jumps November 25, 2020
We use the behavior of the L2 norm of the solutions of linear hyperbolic equations with discontinuous coefficient matrices as a surrogate to infer stability of discontinuous Galerkin spectral element methods (DGSEM). Although the L2 norm is not bounded by the initial data for homogeneous and dissipative boundary conditions for such systems, the L2 norm is easier to work with than a norm that discounts growth due to the discontinuities. We show that the DGSEM with an upwind numerical flux that satisfies the Rankine-Hugoniot (or conservation) condition has the same energy bound as the partial differential equation does in the L2 norm, plus an added dissipation that depends on how much the approximate solution fails to satisfy the Rankine-Hugoniot jump.
Preprint available at arXiv:2011.11746
- New paper submitted: A Sub-Element Adaptive Shock Capturing Approach for Discontinuous Galerkin Methods November 23, 2020
In this paper, a new strategy for a sub-element based shock capturing for discontinuous Galerkin (DG) approximations is presented. The idea is to interpret a DG element as a collection of data and construct a hierarchy of low to high order discretizations on this set of data, including a first order finite volume scheme up to the full order DG scheme. The different DG discretizations are then blended according to sub-element troubled cell indicators, resulting in a final discretization that adaptively blends from low to high order within a single DG element. The goal is to retain as much high order accuracy as possible, even in simulations with very strong shocks, as e.g. presented in the Sedov test. The framework retains the locality of the standard DG scheme and is hence well suited for a combination with adaptive mesh refinement and parallel computing. The numerical tests demonstrate the sub-element adaptive behavior of the new shock capturing approach and its high accuracy.
Preprint available at arXiv:2011.03338.
- Snapshot: 2D Riemann problem computed with a hybrid Discontinuous Galerkin / Finite Volume scheme October 23, 2020
We present a 2D Riemann problem (configuration 3) computed with a hybrid Discontinuous Galerkin / Finite Volume scheme on a uniform grid with 1024^2 degrees of freedom.
In this hybrid approach we are blending an 8th order, 4th order and 2nd order DG as well as a 1st order FV scheme.
- New paper submitted: Preventing pressure oscillations does not fix local linear stability issues of entropy-based split-form high-order schemes September 29, 2020
Recently, it was discovered that the entropy-conserving/dissipative high-order split-form discontinuous Galerkin discretizations have robustness issues when trying to solve the simple density wave propagation example for the compressible Euler equations. The issue is related to missing local linear stability, i.e. the stability of the discretization towards perturbations added to a stable base flow. This is strongly related to an anti-diffusion mechanism, that is inherent in entropy-conserving two-point fluxes, which are a key ingredient for the high-order discontinuous Galerkin extension. In this paper, we investigate if pressure equilibrium preservation is a remedy to these recently found local linear stability issues of entropy-conservative/dissipative high-order split-form discontinuous Galerkin methods for the compressible Euler equations. Pressure equilibrium preservation describes the property of a discretization to keep pressure and velocity constant for pure density wave propagation. We present the full theoretical derivation, analysis, and show corresponding numerical results to underline our findings. The source code to reproduce all numerical experiments presented in this article is available online (DOI: 10.5281/zenodo.4054366).
Preprint available at arXiv:2009.13139. Numerical results were obtained with Trixi.jl.
- Snapshot: Purely hyperbolic gravity simulations with Trixi.jl September 28, 2020
One of the challenges when simulating astrophysical flows with self-gravity is to compute the gravitational forces. In contrast to the hyperbolic compressible Euler equations, the gravity field is described by an elliptic Poisson equation. In [1], we present a purely hyperbolic approach by reformulating the elliptic problem into a hyperbolic diffusion problem, which is solved in pseudotime using the same explicit high-order discontinuous Galerkin method we use for the flow solution.
We start with the Poisson equation for the Newtonian gravitational potential $\phi$,
$$-\vec{\nabla}^2\phi = -4\pi G \rho\label{grav}$$
where G is the universal gravitational constant and $\rho$ is the mass density. Following Nishikawa’s work, we convert the Poisson equation for the gravitational potential into the hyperbolic gravity equations,
$$\frac{\partial}{\partial t}\begin{bmatrix}
\phi\\[0.1cm]
q_1\\[0.1cm]
q_2\\[0.1cm]
\end{bmatrix}
+
\frac{\partial}{\partial x}\begin{bmatrix}
-q_1\\[0.1cm]
-\phi/T_r\\[0.1cm]
0\\[0.1cm]
\end{bmatrix}
+
\frac{\partial}{\partial y}\begin{bmatrix}
-q_2\\[0.1cm]
0\\[0.1cm]
-\phi/T_r\\[0.1cm]
\end{bmatrix}
=
\begin{bmatrix}
-4\pi G \rho\\[0.1cm]
-q_1/T_r\\[0.1cm]
-q_2/T_r\\[0.1cm]
\end{bmatrix},\label{hyp}$$where the auxiliary variables $(q_1,q_2)^\intercal\approx\vec{\nabla}\phi$ and $T_r$ is the relaxation time. The steady-state solution of the hyperbolic system is, in fact, the desired solution of the original Poisson problem.
The flow and the gravity solvers operate on a joint hierarchical Cartesian mesh and are two-way coupled in each Runge-Kutta stage via the source terms. A key benefit of our strategy is that it allows the reuse of existing explicit hyperbolic solvers without modifications, while retaining their advanced features such as non-conforming and solution-adaptive grids.
We implemented this purely hyperbolic approach for self-gravitating gas dynamics in Trixi.jl, a tree-based numerical simulation framework for hyperbolic PDEs, which is written in Julia [2]. It was first validated by computing the Jeans gravitational instability, which demonstrates excellent agreement of the numerical results with the analytical solution:
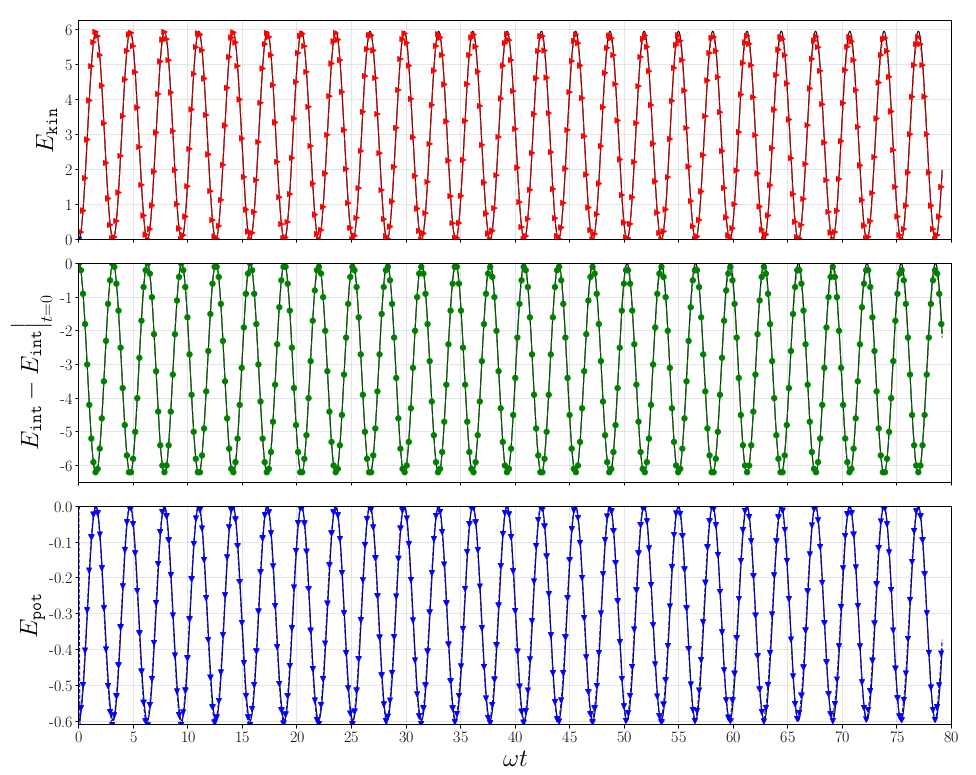
Evolution of the computed kinetic, internal, and potential energies for the Jeans
instability using polynomial order N = 3 on a uniform 16 × 16 mesh. The analytical energies are included for reference.In a second example, we consider a modification of the Sedov blast wave problem that incorporates the effects of gravitational acceleration and which involves strong shocks and complex fluid interactions. We include it to demonstrate the shock capturing and AMR capabilities of Trixi.jl to resolve the cylindrical Sedov blast wave:
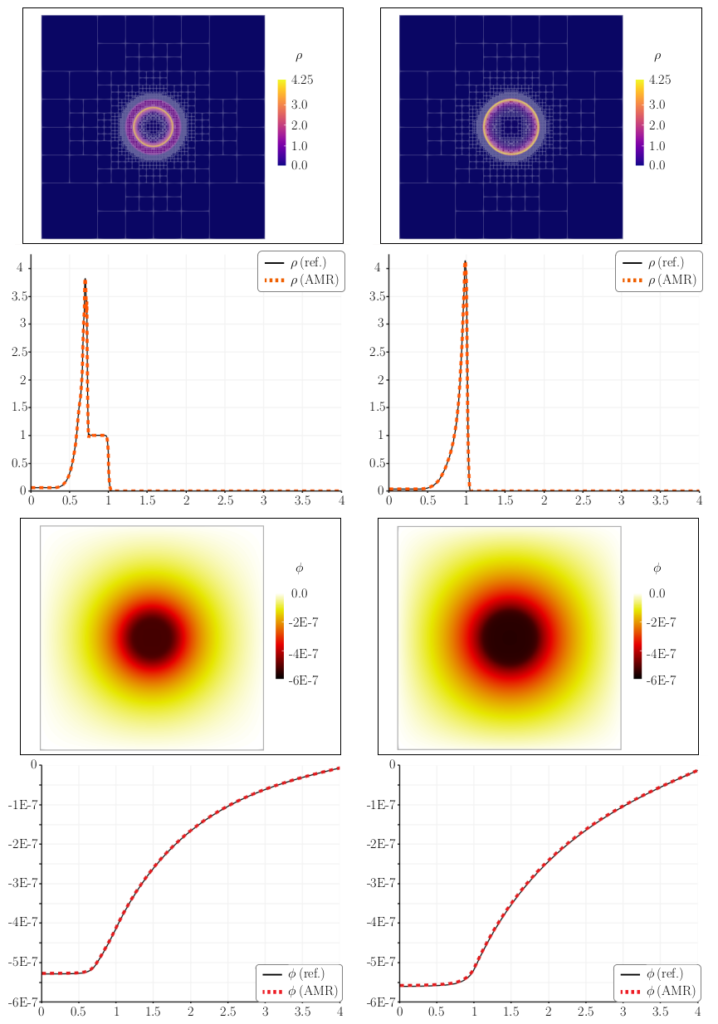
Self-gravitating Sedov explosion approximated with polynomial order $N = 3$ on an AMR grid with four levels of possible refinement at $T = 0.5$ (left) and $T = 1.0$ (right). (first and third row) Two dimensional plots of the density and gravitational potential at two times. The white overlay of squares in the density plots shows the AMR grids used by both solvers. (second and last row) One dimensional slices of the solutions along a line from the origin to the edge of the domain in the positive x-direction. Finally, we show the evolution of the solution together with the adaptive mesh, which is dynamically refined and coarsened to maintain high accuracy while reducing the overall computation time:
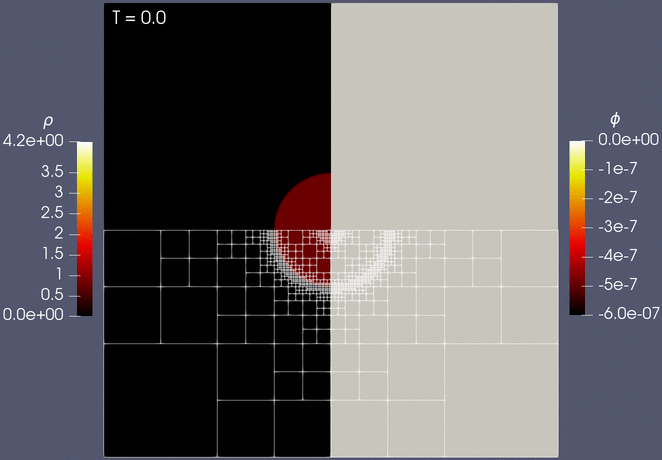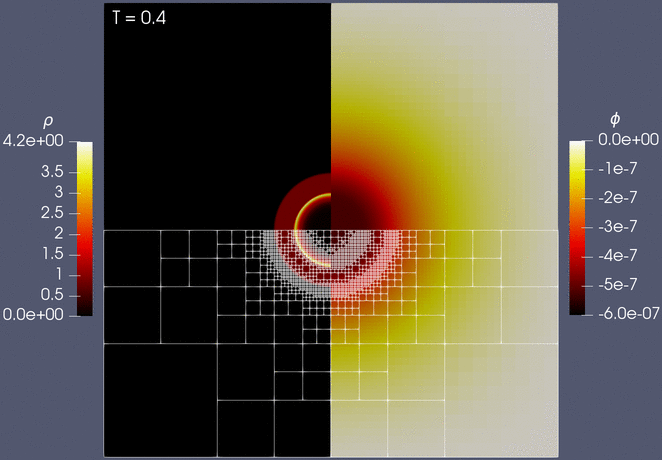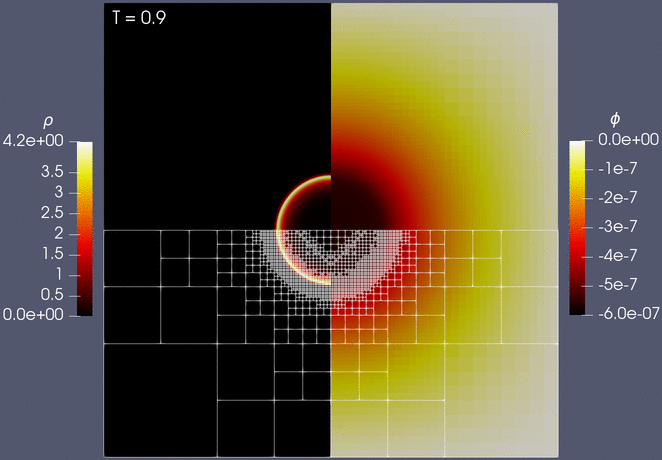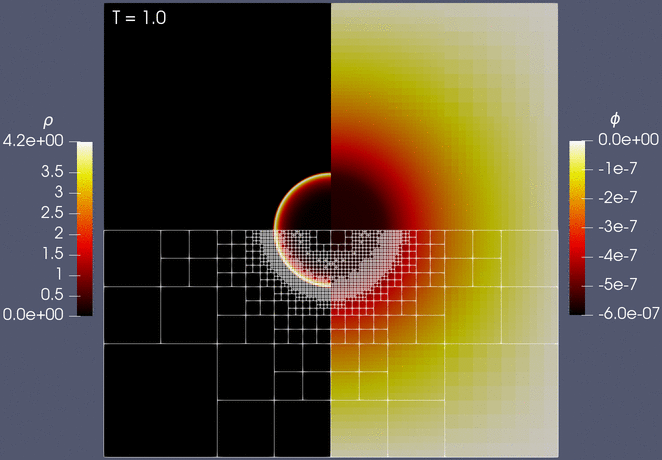
Simulation of self-gravitating Sedov blast wave with adaptive mesh refinement, where adaptation performed after every time step of the compressible Euler solver. The total run time compared to a uniformly refined mesh is reduced by a factor of 19, while the solutions are virtually unchanged. All results in the paper can be easily reproduced by using the resources provided in [3], including step-by-step instructions for how to obtain and install Trixi.jl.
References
[1] Schlottke-Lakemper, Michael and Winters, Andrew R and Ranocha, Hendrik and Gassner, Gregor J, A purely hyperbolic discontinuous Galerkin approach for self-gravitating gas dynamics, submitted to J Comp Phys, 2020. arXiv:2008.10593
[2] Schlottke-Lakemper, Michael and Gassner, Gregor J and Ranocha, Hendrik and Winters, Andrew R, Trixi.jl: A tree-based numerical simulation framework for hyperbolic PDEs written in Julia, 2020. doi:10.5281/zenodo.3996439
[3] Schlottke-Lakemper, Michael and Winters, Andrew R and Ranocha, Hendrik and Gassner, Gregor J, Self-gravitating gas dynamics simulations with Trixi.jl, 2020. doi:10.5281/zenodo.3996575
- Trixi.jl: A tree-based numerical simulation framework for hyperbolic PDEs written in Julia September 1, 2020
Trixi.jl is a numerical simulation framework for hyperbolic conservation laws written in Julia. A key objective for the framework is to be useful to both scientists and students. Therefore, next to having an extensible design with a fast implementation, Trixi is focused on being easy to use for new or inexperienced users, including the installation and postprocessing procedures. Its features include:
- Hierarchical quadtree/octree grid with adaptive mesh refinement
- Native support for 2D and 3D simulations
- High-order accuracy in space in time
- Nodal discontinuous Galerkin spectral element methods
- Kinetic energy-preserving and entropy-stable split forms
- Entropy-stable shock capturing
- Explicit low-storage Runge-Kutta time integration
- Square/cubic domains with periodic and Dirichlet boundary conditions
- Multiple governing equations:
- Compressible Euler equations
- Magnetohydrodynamics equations
- Hyperbolic diffusion equations for elliptic problems
- Scalar advection
- Multi-physics simulations
- Shared-memory parallelization via multithreading
- Visualization of results with Julia-only tools (2D) or ParaView/VisIt (2D/3D)
Trixi.jl was initiated by Michael Schlottke-Lakemper and Gregor Gassner (both University of Cologne, Germany). Together with Hendrik Ranocha (KAUST, Saudi Arabia) and Andrew Winters (Linköping University, Sweden), they are the principal developers of Trixi.
In case of questions, please feel free to create an issue. We are looking forward to feedback and/or potential scientific collaboration.
- New paper submitted: A purely hyperbolic discontinuous Galerkin approach for self-gravitating gas dynamics August 26, 2020
One of the challenges when simulating astrophysical flows with self-gravity is to compute the gravitational forces. In contrast to the hyperbolic hydrodynamic equations, the gravity field is described by an elliptic Poisson equation. We present a purely hyperbolic approach by reformulating the elliptic problem into a hyperbolic diffusion problem, which is solved in pseudotime using the same explicit high-order discontinuous Galerkin method we use for the flow solution. The flow and the gravity solvers operate on a joint hierarchical Cartesian mesh and are two-way coupled via the source terms. A key benefit of our approach is that it allows the reuse of existing explicit hyperbolic solvers without modifications, while retaining their advanced features such as non-conforming and solution-adaptive grids. By updating the gravitational field in each Runge-Kutta stage of the hydrodynamics solver, high-order convergence is achieved even in coupled multi-physics simulations. After verifying the expected order of convergence for single-physics and multi-physics setups, we validate our approach by a simulation of the Jeans gravitational instability. Furthermore, we demonstrate the full capabilities of our numerical framework by computing a self-gravitating Sedov blast with shock capturing in the flow solver and adaptive mesh refinement for the entire coupled system.
Available at arXiv:2008.10593
- Snapshot: A new approach for approximating conservation laws August 24, 2020
A new approach for approximating conservation laws has been tested: instead of monitoring the changes of the means of a quantity within a certain volume over time like a finite volume procedure, this method mimics the behavior of simple solutions.
First the current state is split into waves w, each aligned along one of the eigenvectors of the Fluxjacobian and living on its own grid. Then the corresponding grids are being moved with their eigenvelocity and finally all waves w are being overlayed and normalized yielding the solution after one timestep.
The plots show the solution of isothermal Euler equations at Time T=0.0000 (initial condition) and T=0.0025 with N=40 gridpoints for each mesh.
- Snapshot: Higher-order schemes for the MHD equations July 31, 2020
A robust and easy way of simulating a hyperbolic test case with discontinuities is to use a 1st order finite volume scheme. Using such a method for magnetohydrodynamics (MHD) problems like the Orszag-Tang vortex leads to following results:
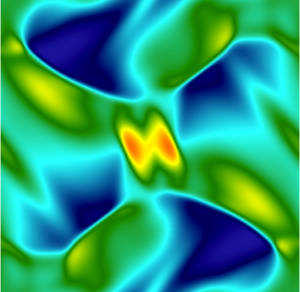
For this and the following examples we used a 4th order time integration scheme and 256 degrees of freedom in each spatial direction.A way to generate more accurate results is to increase the order of the scheme, which has to be treated with caution near discontinuities because oscillations may occur. To overcome this issue one could use higher order schemes in smooth regions and lower order schemes in regions with discontinuities. An example for such an approach is our so called DGFV scheme, which blends e.g. a 4th order Discontinuous Galerkin scheme with a 1st order Finite Volume scheme.
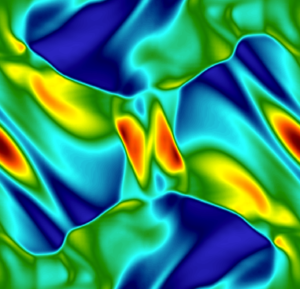
Another way of doing it, is to use a suitable 4th order finite-volume scheme for MHD with a fitting limiter.
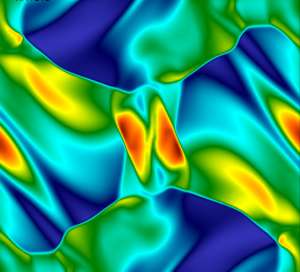
- New paper published: Entropy-Stable p-Nonconforming Discretizations with the Summation-by-Parts Property for the Compressible Navier–Stokes Equations July 16, 2020
The entropy-conservative/stable, curvilinear, nonconforming, p-refinement algorithm for hyperbolic conservation laws of Del Rey Fernández et al. (2019) is extended from the compressible Euler equations to the compressible Navier–Stokes equations. A simple and flexible coupling procedure with planar interpolation operators between adjoining nonconforming elements is used. Curvilinear volume metric terms are numerically approximated via a minimization procedure and satisfy the discrete geometric conservation law conditions. Distinct curvilinear surface metrics are used on the adjoining interfaces to construct the interface coupling terms, thereby localizing the discrete geometric conservation law constraints to each individual element. The resulting scheme is entropy conservative/stable, element-wise conservative, and freestream preserving. Viscous interface dissipation operators that retain the entropy stability of the base scheme are developed. The accuracy and stability of the resulting numerical scheme are shown to be comparable to those of the original conforming scheme in Carpenter et al. (2014) and Parsani et al. (2016), i.e., this scheme achieves ~p+1/2 convergence on geometrically high-order distorted element grids; this is demonstrated in the context of the viscous shock problem, the Taylor–Green vortex problem at a Reynolds number of Re = 1,600 and a subsonic turbulent flow past a sphere at Re = 2,000.
- New article published in ECCOMAS Newsletter (p.16-20): Split Form Discontinuous Galerkin Methods For Implicit Large Eddy Simulation Of Compressible Turbulence July 16, 2020
As a teaser we show a numerical demonstration of the capabilities of the split form DG approach. We consider the flow past a plunging SD7003 airfoil at Mach number and cord length based Reynolds number Rec = 40,000. We subdivide the computational domain into 58,490 unstructured curvilinear hexahedral elements and use a polynomial degree N = 7 resulting in a total of about 150 million degrees of freedom.
The Newsletter is available via: eccomas Newsletter.
- Snapshot: Variant of the Boss-Bodenheimer test with a self-gravitating high order hydro code June 26, 2020
Variant of the classical Boss-Bodenheimer Test: We simulate the collapse and fragmentation of a rotating cloud core using a Discontinous Galerkin / Finite Volume hybrid high-order code. The self-gravity of the gas is calculated via the Fast-Multipole-Method.
- Snapshot: 2D PyOpenGL real-time simulation of the forward-facing step test case May 27, 2020
WENO methods refers to a class of nonlinear finite volume or finite difference methods which are well suited to approximate solutions of hyperbolic conservation laws with high order accuracy in smooth regions and essentially non-oscillatory transition for solution discontinuities. In the following video we used a 5th order accurate WENO-FD scheme with immersed boundary conditions.
Here we solve the forward-facing step test case in real-time using Python3/PyOpenGL/GLFW with an Intel Corporation HD Graphics 620 (rev 02). As one can see, it is also possible to add pressure peaks to the simulation by simply clicking with the mouse on the desired field.
- Snapshot: Smoothed-Particle Hydrodynamics (SPH) simulation of the Numerical Simulation Research Group April 28, 2020
Smoothed-particle hydrodynamics (SPH) is a computational method used for simulating the mechanics of continuum media, such as solid mechanics and is being increasingly used to model fluid motion as well.
This method is well-suited for problems dominated by complex boundary dynamics, since SPH is a mesh-free method, as well as for mass conservation problems since the particles themselves represent mass.We used a 2D Python/OpenCL SPH code that solves the incompressible Navier-Stokes equations in real time. In this simulation, 52,700 particles were used to smash the people of the Numerical Simulation Research Group against each other.
- Snapshot: Blast wave simulation computed in FLUXO with an entropy-stable high-order Discontinuous Galerkin/Finite Volume hybrid scheme March 9, 2020
Blast wave simulation with periodic boundaries computed in FLUXO with an
entropy-stable high-order Discontinuous Galerkin/Finite Volume scheme.The scheme is formulated in Hennemann and Gassner. “A provably entropy stable subcell shock capturing approach for high order split form DG.” Journal of Computational Physics (submitted). The scheme computes the spatial operator as F = (1-a) F_{DG} + a F_{FV}, where a is the blending function
- Talk: Lea Miko Versbach, Lund University, Sweden, “Implicit DG solvers and multigrid preconditioners” [05.02.2020, 11am] February 4, 2020
On Wednesday, 5 February 2020 at 11:00 Lea Miko Versbach will talk on the topic “Implicit DG solvers and multigrid preconditioners”
Location: Gyrhofstraße 8a (Gebäude 158a), Room 1.105 (1st floor), 50931
Abstract: In this talk I will give an introduction to implicit DG solvers and the challenges which arise when solving the large nonlinear systems coming from the implicit temporal discretization. We will solve these system using a Jacobian-free Newton-Krylov method. The problem with this method is that the Krylov subspace method converges slowly for discretized PDEs. In order to speed up computations, we need to construct preconditioners. This can be done using iterative methods. Carefully constructed multigrid methods are cheap and effective preconditioners. I will explain more details about the construction of these preconditioners and show some numerical results.
- New paper published: Dynamic load balancing for direct-coupled multiphysics simulations January 29, 2020
High parallel efficiency for large-scale coupled multiphysics simulations requires the computational load to be evenly distributed among all compute cores. For complex applications and massively parallel computations, even minor load imbalances can have a severe impact on the overall performance and resource usage. Exemplarily for a volume-coupled multiphysics simulation, a direct-hybrid method is considered, in which a CFD and a CAA simulation are performed concurrently on the same parallel subdomains. For differing load compositions on each subdomain, accurate computational weights for CFD and CAA cells must be known to determine an efficient domain decomposition. Therefore, a dynamic load balancing scheme is presented, which allows to increase the efficiency of complex coupled simulations with non-trivial domain decompositions. A fully-coupled three-dimensional jet simulation with approximately 300 million degrees of freedom demonstrates the effectiveness of the approach to reduce load imbalances. A detailed performance analysis substantiates the necessity of dynamic load balancing. Furthermore, the results of a strong scaling experiment show the benefit of load balancing to be proportional to the degree of parallelism. In addition, it is shown that the approach allows to attenuate imbalances also for parallel computations on heterogeneous computing hardware. The acoustic field of a chevron nozzle will also be discussed.
- Talk: Bernhard Müller, Department of Energy and Process Engineering, Norwegian University of Science and Technology (NTNU), Trondheim, Norway [04.02.2020, 11am] January 28, 2020
On Tuesday, 4 February 2020 at 11:00 Bernhard Müller will talk on the topic “Immersed Boundary Method for the Compressible Navier-Stokes Equations Using High Order Summation-By-Parts Operators” based on a joint work with M. Ehsan Khalili and Knut Emil Ringstad, NTNU, and Martin Larsson, Sportradar AS, Trondheim.
Location: Gyrhofstraße 8a (building 158a), Room 1.105 (1st floor), 50931 Cologne
Abstract: An efficient and versatile immersed boundary method (IBM) for simulating compressible viscous flows with complex and moving convex boundaries has been developed. The compressible Navier-Stokes equations are discretized by globally fourth order summation-by-parts (SBP) difference operators with in-built stability properties and the classical fourth order explicit Runge-Kutta method. The proposed Cartesian grid based IBM builds on the ghost point approach in which the solid wall boundary conditions are applied as sharp interface conditions. The interpolation of the flow variables at image points and the solid wall boundary conditions are used to determine the flow variables at three layers of ghost points within the solid body in order to introduce the presence of the body interface in the flow computation and to maintain the overall high order of accuracy of the flow solver. Two different reconstruction procedures, bilinear interpolation and weighted least squares method, are implemented to obtain the values at the ghost points. A robust high order immersed boundary method is achieved by using a hybrid approach in which the first layer of ghost points is treated by using a third order polynomial combined with the weighted least squares method and the second and third layers of ghost points are treated by using bilinear interpolation to find the values at the image points of the corresponding ghost points. After demonstrating the accuracy of the present IBM for low Mach number flow around a circular cylinder, it is applied to simulate flow in the cross-section of the upper airways of a specific obstructive sleep apnea patient. The IBM solver has been further verified and validated for moving boundaries by applying it to a transversely oscillating cylinder in freestream flow and an in-line oscillating cylinder in an initially quiescent fluid. Sound waves generated by the in-line oscillation of the cylinder exhibit both quadrupole and monopole types. The present IBM is also verified for fluid-structure interaction of an elastically mounted circular cylinder in freestream flow at Reynolds number 200, and the rate of energy transferred between the fluid and the structure is investigated. - Snapshot: Postdoctoral researcher Dr. Andrés Rueda-Ramírez joins our research group January 24, 2020

Andrés M. Rueda-Ramírez completed his undergraduate studies in Mechanical Engineering at the National University of Colombia (Universidad Nacional de Colombia, UNAL). After graduating, he worked as a research and teaching assistant at the Research Group on biomechanics at UNAL, where he collaborated with a highly interdisciplinary team in the development of a Finite Element software to simulate bone growing processes.
AMRR completed his Ph.D. studies in Aerospace Engineering at the Polytechnic University of Madrid (Universidad Politécnica de Madrid). During his Ph.D., AMRR studied and developed p-adaptation algorithms, implicit time-integration schemes, and multigrid solvers for high-order Discontinuous Galerkin Spectral Element Methods (DGSEM).
AMRR is now a member of the Numerical Simulation Research Group at the University of Cologne, where he joined the development team of the DGSEM code FLUXO. AMRR is currently working on sub-cell shock-capturing schemes and time integrators for the Navier-Stokes and the MHD equations.
- Talk: Ruediger Pakmor, Max-Planck-Institute for Astrophysics, Garching January 24, 2020
On Friday, 31 January 2020 at 14:00 Ruediger Pakmor will talk on the topic “The numerical schemes behind the moving mesh code Arepo”
Location: Weyertal 86-90, Seminar room 1 (ground floor), 50931 Cologne
Abstract: I will present the schemes behind the moving mesh magnetohydrodynamics code Arepo and discuss in particular the finite volume scheme on a moving mesh and its time integration. I will then show an example of an anisotropic diffusion solver on the unstructured Voronoi mesh used in Arepo and discuss general properties of the Arepo code.
- Talk: Cedrick Ansorge, Institut für Geophysik und Meteorologie, Universität zu Köln January 21, 2020
On Tuesday, 28 January 2020 at 11.00 Cedrick Ansorge will talk on the topic “Turbulent Ekman flow as virtual lab in geophysical fluid dynamics”
Location: Gyrhofstraße 8a (Gebäude 158a), Room 1.105 (1st floor), 50931 Cologne
Abstract: The atmospheric boundary layer (ABL) is the lowest part of the atmosphere that is directly linked to the surface through vertical turbulent exchange, typically the lowest 100 to 1000m. There, turbulent mixing is the main vertical transport mechanism for heat, water, momentum and any kind of air constituent. Besides turbulence, the ABL is a multi-physical system comprising also radiative, miro-physical, chemical and other processes on scales from the multi-kilometre range down to the Kolmogorov scale of turbulent motion at the sub-millimetre range in three spatial dimensions. Both the multiphysical complexity and the broad-scale nature are prohibitive for a brute-force approach to numerical modelling of the system. Truncated representations of the ABL are thus inevitable when numerically modeling the ABL.
I will introduce turbulent Ekman flow–the doubly periodic flow over a flat rotating plate—that physically truncates the ABL to its fluid-mechanical core, the Navier–Stokes equations with appropriate boundary conditions. The governing equations are solved by a highly scalable numerical algorithm that is being used on up to 250,000 compute cores to represent the turbulent flow on grids that routinely use 3 × 230 collocation points in space. The reduced physical complexity allows for high-fidelity turbulence simulations where the entire range of turbulent motion is represented directly–without need for turbulence closure. We can thus study the ABL under conditions for which classical approaches to represent turbulence fail–such as partial or complete laminarization and transitional flows.
- New paper submitted: A Sub-Element Adaptive Shock Capturing Approach for Discontinuous Galerkin Methods December 18, 2019
In this paper,a new strategy for a sub-element based shock capturing for discontinuous Galerkin (DG) approximations is presented. The idea is to interpret a DG element as a collection of data and construct a hierarchy of low to high order discretisations on this set of data, including a first order finite volume (FV) scheme up to the full order DG scheme. The different DG discretisations are then blended according to sub-element troubled cell indicators, resulting in a final discretisation that adaptively blends from low to high order within a single DG element. The goal is to retain as much high order accuracy as possible, even in simulations with very strong shocks, as e.g. presented in the Sedov test. The framework retains the locality of the standard DG scheme and is hence well suited for a combination with adaptive mesh refinement (AMR) and parallel computing. The numerical tests demonstrate the sub-element adaptive behaviour of the new shock capturing approach and its high accuracy.
- Talk: Almut Gassmann, Leibnitz-Institute of Atmospheric Physics, University Rostock December 12, 2019
On Friday, 13 December 2019 at 14.00 Almut Gassman will talk on the topic “Entropy production in numerical modeling of a moist atmosphere”
Location: Weyertal 86 – 90, Seminar room 1 (ground floor), 50931 Cologne
Abstract: Atmospheric models are based on basic physical laws, like mass conservation, momentum conservation or sometimes energy conservation. In this talk, another law is inspected, namely the second law of thermodynamics which says that the internal entropy production has to be positive. This law has hardly been checked by modellers. But this law determines the direction (but not the strength) of subgrid-scale parameterized fluxes. Furthermore, the choice of numerical schemes for advection is also limited, because the inherent diffusion of those schemes must be downgradient with respect to the gradients of special measures, which are determined by the second law. The formulation of energetically and entropically consistent numerical schemes will be outlined. Examples of failure of contemporary schemes with respect to the second law will be shown. For instance, conventional (non-entropy-consistent) heat flux parameterizations in the mesosphere will amplify waves instead of allowing them to break and dissipate. Or, as another example, entropy-law-inconsistent higher order or TVD advection schemes for temperature might give rise to accelerations of the wind in the wrong direction. When inspecting the different entropy production (or dissipation) rates in the atmosphere, four types of those rates are distinguished, namely (i) dissipation due to friction, (ii) dissipation due to heat fluxes, (iii) dissipation due to mixing of constituents, and (iv) dissipation due to phase changes. The most important among them are the dissipation due to friction and the dissipation due to falling rain, which can be seen as a special case of mixing of moist air and precipitation.
- Snapshot of the month: Supersonic 3D Blob November 15, 2019