The discontinuous Galerkin spectral element method (DGSEM) is a nodal discontinuous Galerkin collocation scheme that uses a set of Legendre-Gauss or Legendre-Gauss-Lobatto nodes to represent the solution with Lagrange interpolating polynomials and to compute integrals with a quadrature rule.

It was recently shown [1] that the DGSEM semi-discretization of a conservation law using Legendre-Gauss nodes can be written in finite-volume form as
\begin{equation*}
J_{j} \dot{\mathbf{u}}^{DG}_{j} =
\frac{1}{\omega_j}
\left(
\hat{\mathbf{f}}^{DG}_{(j-1,j)}
– \hat{\mathbf{f}}^{DG}_{(j,j+1)}
\right),
\end{equation*}
where $J_j$ is the mapping Jacobian, $\omega_j$ are the Legendre-Gauss quadrature weights, and $\hat{\mathbf{f}}^{DG}_{(\cdot,\cdot)}$ are high-order DGSEM fluxes between adjacent nodes.

The existence of a FV form for the Legendre–Gauss DGSEM enables the use of the subcell limiting strategies described in [2]. In these methods, a hybrid DGSEM/FV method is used, where the semi-discretization at each node reads
\begin{equation*}
J_{j} \dot{\mathbf{u}}_{j} =
\frac{1}{\omega_j}
\left(
\hat{\mathbf{f}}_{(j-1,j)}
– \hat{\mathbf{f}}_{(j,j+1)}
\right),
\end{equation*}
and the local fluxes are obtained as a convex combination of high-order DGSEM and low-order FV fluxes,
\begin{equation*}
\hat{\mathbf{f}}_{(i,j)} = (1-\alpha_{(i,j)}) \hat{\mathbf{f}}^{DG}_{(i,j)}
+
\alpha_{(i,j)}
\hat{\mathbf{f}}^{DG}_{(i,j)},
~~~~
\alpha_{(i,j)} \in [0,1].
\end{equation*}

To illustrate the shock-capturing capacity of the hybrid DGSEM/FV method, we simulate a Sedov blast problem describing the evolution of a blast wave expanding from an initial concentration of density and pressure, and adjust the blending coefficient $\alpha_{(i,j)}$ to avoid non-physical density oscillations in the vicinity of shocks.

The video shows the distribution of density and the blending coefficient obtained for entropy-stable variants of the Legendre-Gauss and Legendre-Gauss-Lobatto DGSEM methods.

The simulation runs stably without any spurious oscillations for both variants of the DGSEM method.
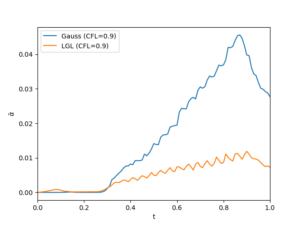
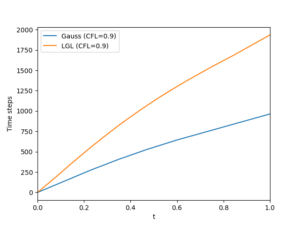
The figures below show the mean blending coefficient and the number of time steps for the simulation of the blast wave.
Although the Legendre–Gauss DGSEM requires more limiting than the Legendre-Gauss-Lobatto DGSEM to avoid spurious density oscillations, it completes the simulation in fewer time steps.
The Legendre-Gauss subcell distribution allows for longer time-step sizes than the Legendre-Gauss-Lobatto subcell distribution for the same CFL number.

Mean blending coefficient

Number of time steps

Figure 1: Evolution of the mean blending coefficient and number of time steps taken for the simulation of the blast wave with CFL=0.9.

References
[1] Mateo-Gabín, A., Rueda-Ramírez, A. M., Valero, E., & Rubio, G. (2022). Entropy-stable flux-differencing formulation with Gauss nodes for the DGSEM. arXiv preprint arXiv:2211.05066.
[2] Rueda-Ramírez, A. M., Pazner, W., & Gassner, G. J. (2022). Subcell limiting strategies for discontinuous Galerkin spectral element methods. Computers & Fluids, 247, 105627. arXiv preprint arXiv:2202.00576.