Abstract:

We use the behavior of the L2 norm of the solutions of linear hyperbolic equations with discontinuous coefficient matrices as a surrogate to infer stability of discontinuous Galerkin spectral element methods (DGSEM). Although the L2 norm is not bounded by the initial data for homogeneous and dissipative boundary conditions for such systems, the L2 norm is easier to work with than a norm that discounts growth due to the discontinuities. We show that the DGSEM with an upwind numerical flux that satisfies the Rankine-Hugoniot (or conservation) condition has the same energy bound as the partial differential equation does in the L2 norm, plus an added dissipation that depends on how much the approximate solution fails to satisfy the Rankine-Hugoniot jump.

Accepted in Journal of Scientific Computing.

arXiv link: https://arxiv.org/abs/2011.11746

The second paper of this series presents two robust entropy stable shock-capturing methods for discontinuous Galerkin spectral element (DGSEM) discretizations of the compressible magneto-hydrodynamics (MHD) equations. Specifically, we use the resistive GLM-MHD equations, which include a divergence cleaning mechanism that is based on a generalized Lagrange multiplier (GLM). For the continuous entropy analysis to hold, and due to the divergence-free constraint on the magnetic field, the GLM-MHD system requires the use of non-conservative terms, which need special treatment.

Hennemann et al. [DOI:10.1016/j.jcp.2020.109935] recently presented an entropy stable shock-capturing strategy for DGSEM discretizations of the Euler equations that blends the DGSEM scheme with a subcell first-order finite volume (FV) method. Our first contribution is the extension of the method of Hennemann et al. to systems with non-conservative terms, such as the GLM-MHD equations. In our approach, the advective and non-conservative terms of the equations are discretized with a hybrid FV/DGSEM scheme, whereas the visco-resistive terms are discretized only with the high-order DGSEM method. We prove that the extended method is entropy stable on three-dimensional unstructured curvilinear meshes. Our second contribution is the derivation and analysis of a second entropy stable shock-capturing method that provides enhanced resolution by using a subcell reconstruction procedure that is carefully built to ensure entropy stability.

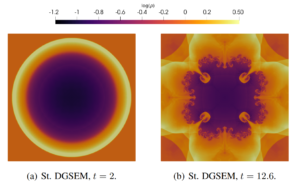
We provide a numerical verification of the properties of the hybrid FV/DGSEM schemes on curvilinear meshes and show their robustness and accuracy with common benchmark cases, such as the Orszag-Tang vortex and the GEM reconnection challenge. Finally, we simulate a space physics application: the interaction of Jupiter’s magnetic field with the plasma torus generated by the moon Io.

Preprint available at: arXiv:2012.12040

In this paper we will review a recent emerging paradigm shift in the construction and analysis of high order Discontinuous Galerkin (DG) methods applied to approximate solutions of hyperbolic or mixed hyperbolic-parabolic partial differential equations (PDEs) in computational physics. There is a long history using DG methods to approximate the solution of PDEs in computational physics with successful applications in linear wave propagation, like those governed by Maxwell’s equations, incompressible and compressible fluid and plasma dynamics governed by the Navier-Stokes and the Magnetohydrodynamics equations, or as a solver for ordinary differential equations (ODEs), e.g., in structural mechanics. The DG method amalgamates ideas from several existing methods such as the Finite Element Galerkin method (FEM) and the Finite Volume method (FVM) and is specifically applied to problems with advection dominated properties, such as fast moving fluids or wave propagation. In the numerics community, DG methods are infamous for being computationally complex and, due to their high order nature, as having issues with robustness, i.e., these methods are sometimes prone to crashing easily. In this article we will focus on efficient nodal versions of the DG scheme and present recent ideas to restore its robustness, its connections to and influence by other sectors of the numerical community, such as the finite difference community, and further discuss this young, but rapidly developing research topic by highlighting the main contributions and a closing discussion about possible next lines of research.

Published in: https://www.frontiersin.org/articles/10.3389/fphy.2020.500690/abstract

Front. Phys. | doi: 10.3389/fphy.2020.500690

We present a hybrid continuous and discontinuous Galerkin spectral element approximation that leverages the advantages of each approach. The continuous Galerkin approximation is used on interior element faces where the equation properties are continuous. A discontinuous Galerkin approximation is used at physical boundaries and if there is a jump in properties at a face. The approximation uses a split form of the equations and two-point fluxes to ensure stability for unstructured quadrilateral/hexahedral meshes with curved elements. The approximation is also conservative and constant state preserving on such meshes. Spectral accuracy is obtained for all examples, which include wave scattering at a discontinuous medium boundary.

Preprint available at: arXiv:2012.06510

We use the behavior of the L2 norm of the solutions of linear hyperbolic equations with discontinuous coefficient matrices as a surrogate to infer stability of discontinuous Galerkin spectral element methods (DGSEM). Although the L2 norm is not bounded by the initial data for homogeneous and dissipative boundary conditions for such systems, the L2 norm is easier to work with than a norm that discounts growth due to the discontinuities. We show that the DGSEM with an upwind numerical flux that satisfies the Rankine-Hugoniot (or conservation) condition has the same energy bound as the partial differential equation does in the L2 norm, plus an added dissipation that depends on how much the approximate solution fails to satisfy the Rankine-Hugoniot jump.

Preprint available at arXiv:2011.11746

In this paper, a new strategy for a sub-element based shock capturing for discontinuous Galerkin (DG) approximations is presented. The idea is to interpret a DG element as a collection of data and construct a hierarchy of low to high order discretizations on this set of data, including a first order finite volume scheme up to the full order DG scheme. The different DG discretizations are then blended according to sub-element troubled cell indicators, resulting in a final discretization that adaptively blends from low to high order within a single DG element. The goal is to retain as much high order accuracy as possible, even in simulations with very strong shocks, as e.g. presented in the Sedov test. The framework retains the locality of the standard DG scheme and is hence well suited for a combination with adaptive mesh refinement and parallel computing. The numerical tests demonstrate the sub-element adaptive behavior of the new shock capturing approach and its high accuracy.

Preprint available at arXiv:2011.03338.

Recently, it was discovered that the entropy-conserving/dissipative high-order split-form discontinuous Galerkin discretizations have robustness issues when trying to solve the simple density wave propagation example for the compressible Euler equations. The issue is related to missing local linear stability, i.e. the stability of the discretization towards perturbations added to a stable base flow. This is strongly related to an anti-diffusion mechanism, that is inherent in entropy-conserving two-point fluxes, which are a key ingredient for the high-order discontinuous Galerkin extension. In this paper, we investigate if pressure equilibrium preservation is a remedy to these recently found local linear stability issues of entropy-conservative/dissipative high-order split-form discontinuous Galerkin methods for the compressible Euler equations. Pressure equilibrium preservation describes the property of a discretization to keep pressure and velocity constant for pure density wave propagation. We present the full theoretical derivation, analysis, and show corresponding numerical results to underline our findings. The source code to reproduce all numerical experiments presented in this article is available online (DOI: 10.5281/zenodo.4054366).

Preprint available at arXiv:2009.13139. Numerical results were obtained with Trixi.jl.

One of the challenges when simulating astrophysical flows with self-gravity is to compute the gravitational forces. In contrast to the hyperbolic hydrodynamic equations, the gravity field is described by an elliptic Poisson equation. We present a purely hyperbolic approach by reformulating the elliptic problem into a hyperbolic diffusion problem, which is solved in pseudotime using the same explicit high-order discontinuous Galerkin method we use for the flow solution. The flow and the gravity solvers operate on a joint hierarchical Cartesian mesh and are two-way coupled via the source terms. A key benefit of our approach is that it allows the reuse of existing explicit hyperbolic solvers without modifications, while retaining their advanced features such as non-conforming and solution-adaptive grids. By updating the gravitational field in each Runge-Kutta stage of the hydrodynamics solver, high-order convergence is achieved even in coupled multi-physics simulations. After verifying the expected order of convergence for single-physics and multi-physics setups, we validate our approach by a simulation of the Jeans gravitational instability. Furthermore, we demonstrate the full capabilities of our numerical framework by computing a self-gravitating Sedov blast with shock capturing in the flow solver and adaptive mesh refinement for the entire coupled system.

Available at arXiv:2008.10593

The entropy-conservative/stable, curvilinear, nonconforming, p-refinement algorithm for hyperbolic conservation laws of Del Rey Fernández et al. (2019) is extended from the compressible Euler equations to the compressible Navier–Stokes equations. A simple and flexible coupling procedure with planar interpolation operators between adjoining nonconforming elements is used. Curvilinear volume metric terms are numerically approximated via a minimization procedure and satisfy the discrete geometric conservation law conditions. Distinct curvilinear surface metrics are used on the adjoining interfaces to construct the interface coupling terms, thereby localizing the discrete geometric conservation law constraints to each individual element. The resulting scheme is entropy conservative/stable, element-wise conservative, and freestream preserving. Viscous interface dissipation operators that retain the entropy stability of the base scheme are developed. The accuracy and stability of the resulting numerical scheme are shown to be comparable to those of the original conforming scheme in Carpenter et al. (2014) and Parsani et al. (2016), i.e., this scheme achieves ~p+1/2 convergence on geometrically high-order distorted element grids; this is demonstrated in the context of the viscous shock problem, the Taylor–Green vortex problem at a Reynolds number of Re = 1,600 and a subsonic turbulent flow past a sphere at Re = 2,000.

sciencedirect
arxiv