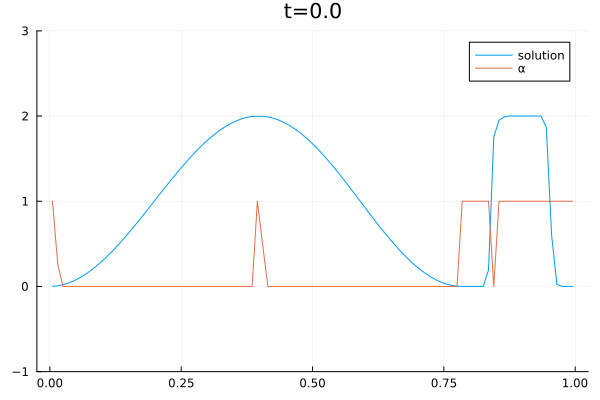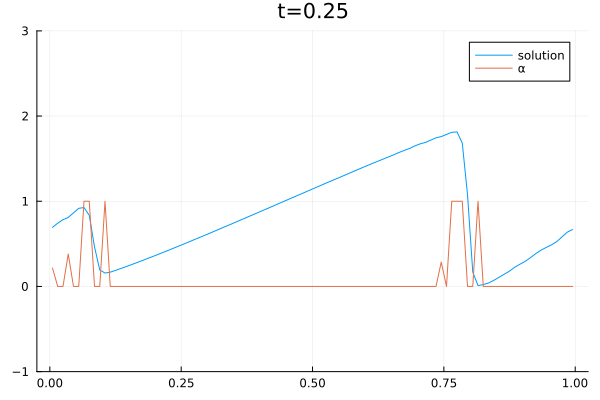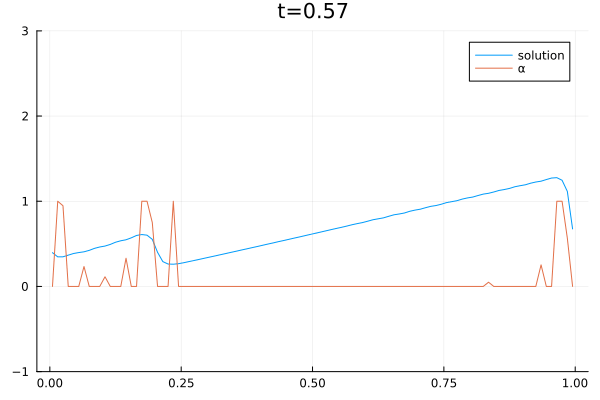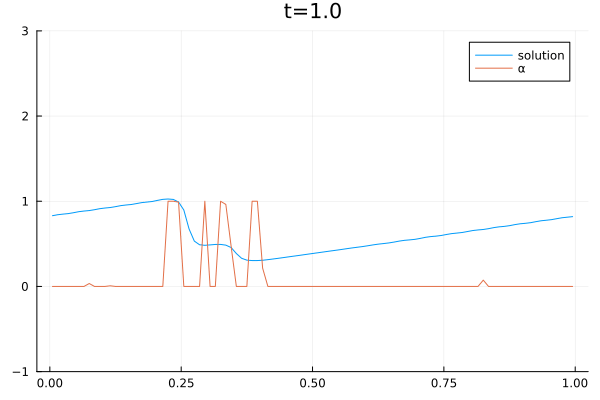
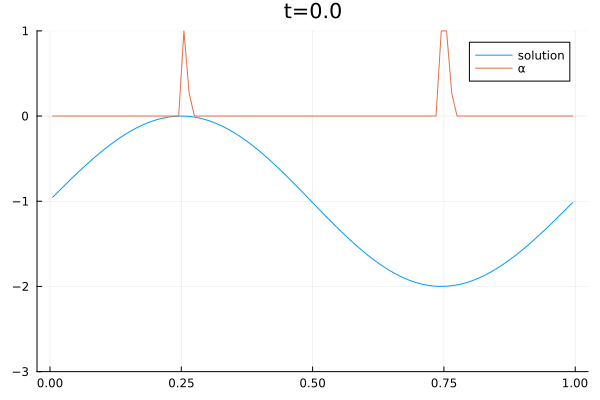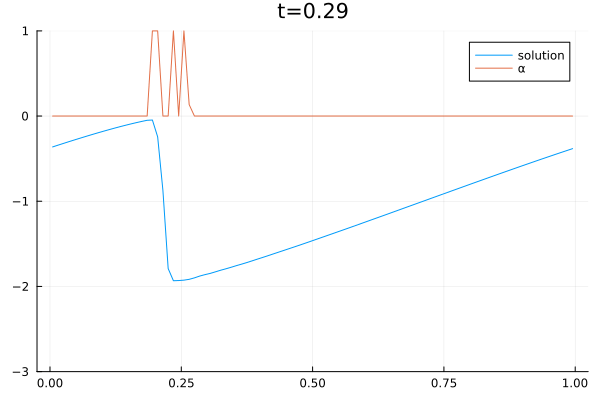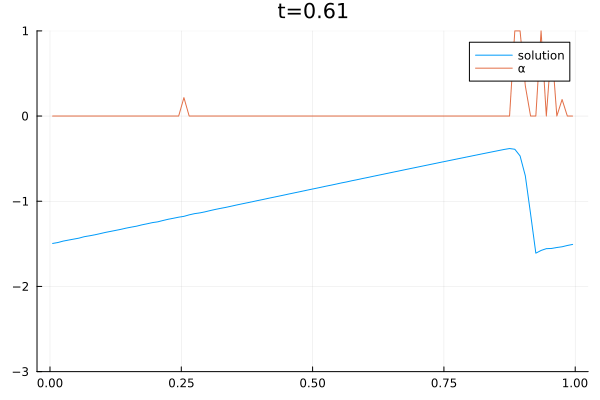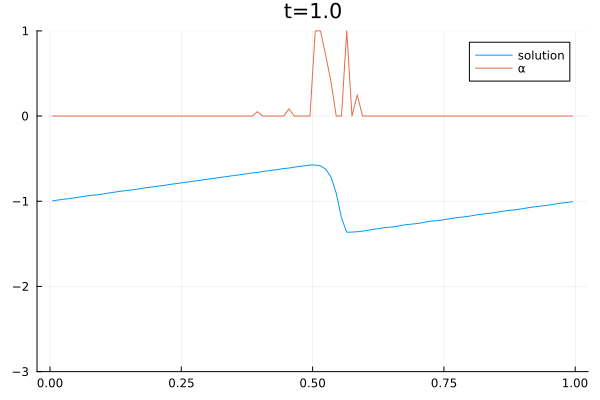
Boqiang Huang received his Ph.D. in Biomedical Engineering from the Department of Electronic Engineering at Fudan University, Shanghai, China, in 2010. Following his doctoral studies, he was awarded the Alexander von Humboldt Postdoctoral Fellowship and worked under the mentorship of Prof. Angela Kunoth. During this time, he contributed as a research scientist in Prof. Kunoth’s group (AG-Kunoth) at the Institute of Mathematics, University of Paderborn, and later at the University of Cologne. In 2021, Dr. Huang joined the group of Prof. Dorit Merhof (AG-Merhof) at the Institute of Imaging and Computer Vision at RWTH Aachen University, and subsequently at the University of Regensburg. His research expertise spans multiple disciplines in the field of data science, including biomedical engineering, electronic engineering, applied mathematics and applied physics.
In July 2024, Dr. Huang became a research scientist in the group of Prof. Gregor Gassner (AG-Gassner). He is also supported by the HESCOR research project (“Human & Earth System Coupled Research” https://hescor.uni-koeln.de/). His current research focuses on the “Machine learning & Culture Clusters” over large timescales, ranging from the Paleolithic era (1.4 million to 24,000 years ago) to the present. He collaborates with researchers from archaeology, geophysics, and the humanities on this interdisciplinary project.