C.2 Behavior View Notations

C.2.1 State Transition Diagrams (STDs)

  

 

Figure C.13:  The Mealy representation of state  transition diagrams.

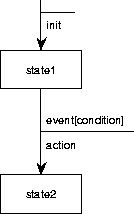TCM supports the Mealy notation for finite state transition diagrams (figure C.13). States are named, and are represented by rectangles.  State transitions are represented by arrows and are labeled by event[condition]/action pairs.    The event is the trigger   of the transition and can be viewed as the occurrence of an input. The condition is a guard.  The precise meaning of the guard depends upon the method in which the notation is used. A minimalistic interpretation is that if the guard is false, an occurrence of the event will not trigger the transition. A more closed interpretation is that additionally, if the guard is true, an occurrence of the event will trigger the transition.

It also depends upon the method what kinds of conditions can occur in the guard. The current version of TCM does not support any method in particular and therefore imposes no constraints on what one can put in a guard.

The action part of the transition label is the output action generated by the transition.

Each Mealy STD must have an initial state, pointed at by an arrow that  leaves from no node, and that can be labeled by an initialization action.  

TCM also has decision points  which are intermediary states that the machine may have between system transactions. Decision points are represented by a hexagon.

Mealy machines are used in Yourdon-style structured analysis, where they are used to specify control processes [23]. The interface of the control process must equal the interface of the Mealy machine. See section C.3.2 for control processes.

C.2.2 Process Structure Diagrams (PSDs)

   

 

Figure C.14:  A process structure diagram.

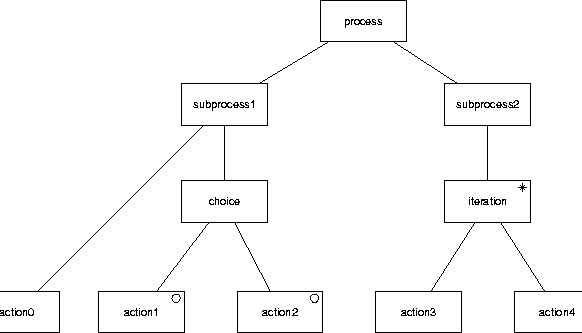Process structure diagrams are used in JSD to represent behavior. A PSD is a tree in which the nodes are labeled [9], [18, chapters 11, 12]. The leaves of the tree represent atomic actions and the root represents the entire process. Sequence is represented by a left-to-right ordering of the children of a node. Iteration is represented by an asterisk label and choice by a small circle in the nodes that represent the options. Figure C.14 gives an example.

PSDs are equivalent to regular expressions.

 

Figure C.15:  A Mealy diagram roughly equivalent to figure C.14.

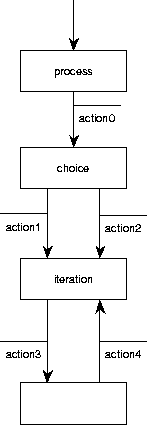A Mealy machine roughly equivalent to this is shown in figure C.15. The names of the nodes in a PSD can be reused as state names in a Mealy STD. However, the Mealy convention forces us to categorize an action as an input or output action, whereas in PSDs this is not the case. In figure C.15 we arbitrarily categorized all PSD actions as output actions.

In JSD, PSDs are used to represent processes in reality and to represent processes in the machine. If used to represent processes in reality, common actions between PSDs represent synchronous communication between these processes. If used to represent processes in the software, communication between processes is represented by means of system network diagrams, described in section C.3.3 below.

C.2.3 Recursive Process Graphs (RPGs)

  

 

Figure C.16:  A recursive process graph.

 

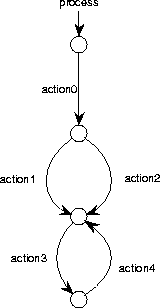Figure C.17:  A recursive process graph with labeled nodes.

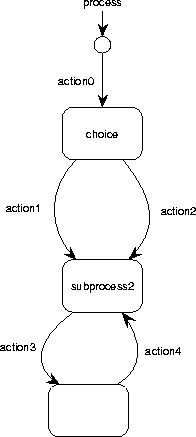A recursive process graph is a rooted directed graph in which the nodes represent states and the edges represent atomic actions or other processes. Figure C.16 shows an RPG equivalent to the PSD of figure C.14. Nodes in RPGs can be labeled, just as in Mealy STDs. Figure C.17 shows an RPG with labeled nodes.

An RPG has an initial node, which is pointed at by a small arrow and  which can be labeled by the name of the process.

 

Figure C.18:  A recursive process graph with a call to another process.

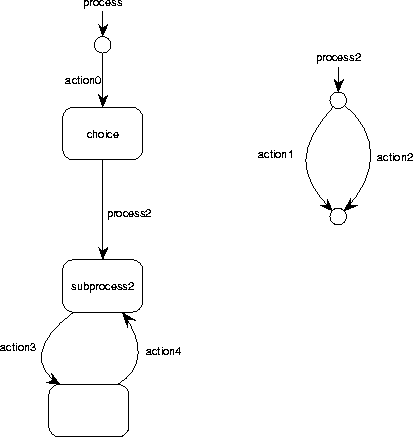An edge in an RPG can be labeled with the name of an action or of a process. If it is labeled with a process name, the transition is equivalent to performing this process. Figure C.18 illustrates this. The RPG in figure C.18 is equivalent to that of figure C.17.

 

Figure C.19:  A recursive process graph with a recursive call.

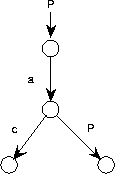The call to another process can be recursive, as illustrated in figure C.19. This describes the process with possible traces 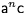${\mbox{\sffamily a}}^n{\mbox{\sffamily c}}$ for $n \geq 1$.

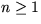Recursive process graphs are defined formally by Spruit and Wieringa [15], based upon the idea of recursive transition networks [21].