Author Archives: Christof Czernik

Snapshot: Astrophysical colliding flow simulation run by a novel Discontinuous Galerkin/Finite Volume (DGFV) blending scheme in FLASH

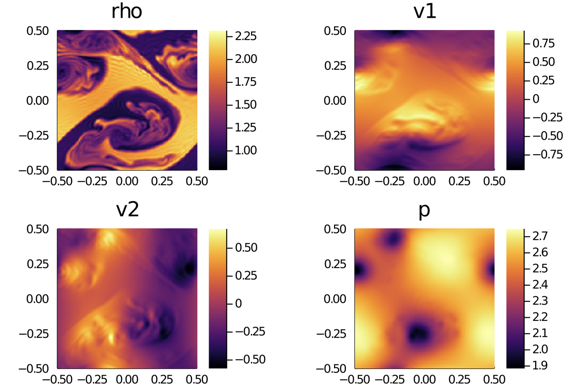
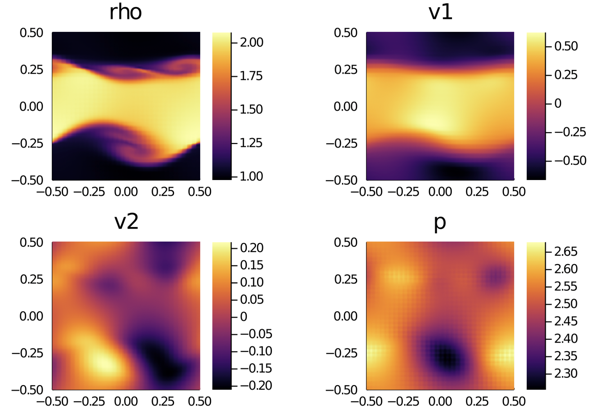
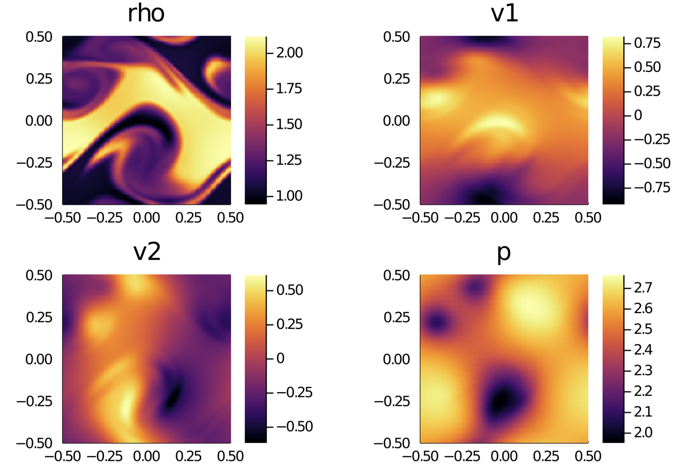
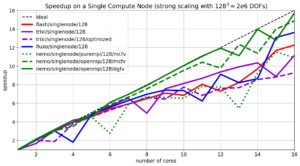
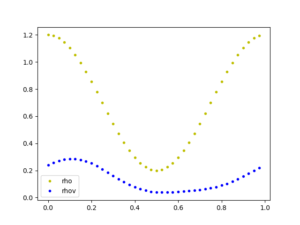
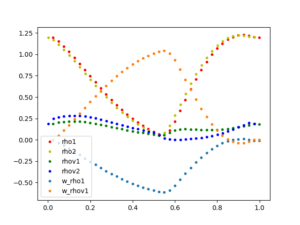
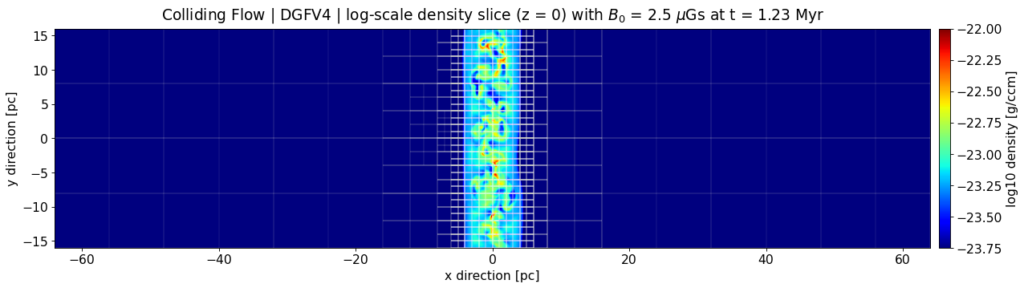
Simulation of an astrophysical colliding flow [1] run by a novel Discontinuous Galerkin/Finite Volume (DGFV) blending scheme [2] which has been implemented in the FLASH code [3].

The code has following capabilities:

  • fourth-order accurate ideal magneto-hydrodynamics with hyperbolic divergence cleaning [4]
  • octree-based adaptive mesh refinement
  • distributive computing and load balancing
  • multi-species fluid dynamics (N_species > 10)
  • turbulent driving
  • octree-based Poisson solver for self-gravity [5]
  • octree-based radiation physics [6]
  • external gravitional fields
  • sink particles [7]
  • chemical reaction networks [8]

[1] Weis, Micheal et al. “The Virial Balance of CO-Substructures in Colliding Magnetised Flows” (in preparation)
[2] Markert, Johannes et al. “A Sub-Element Adaptive Shock Capturing Approach for Discontinuous Galerkin Methods” (submitted)
[3] Fryxell, Bruce, et al. “FLASH: An adaptive mesh hydrodynamics code for modeling astrophysical thermonuclear flashes.” The Astrophysical Journal Supplement Series 131.1 (2000): 273.
[4] Markert, Johannes et al. “Flash goes DG” (working title, in preparation)
[5] Wünsch, Richard, et al. “Tree-based solvers for adaptive mesh refinement code FLASH–I: gravity and optical depths.” Monthly Notices of the Royal Astronomical Society 475.3 (2018): 3393-3418.
[6] Wünsch, Richard et al. “Tree-based solvers for adaptive mesh refinement code FLASH – II: radiation transport module TreeRay” (submitted)
[7] Federrath, Christoph, et al. “Modeling collapse and accretion in turbulent gas clouds: implementation and comparison of sink particles in AMR and SPH.” The Astrophysical Journal 713.1 (2010): 269.
[8] Seifried, D., and S. Walch. “Modelling the chemistry of star-forming filaments–I. H2 and CO chemistry.” Monthly Notices of the Royal Astronomical Society: Letters 459.1 (2016): L11-L15.

 

Snapshot: Accuracy of the LGL-subcell FV scheme with and without inner-element reconstruction

We are interested in the accuracy of the finite volume scheme, on a LGL subcell grid induced by a LGL-DGSEM discretization. For comparison, we look at a Kelvin-Helmholtz-Instability test problem, simulated with 4² LGL nodes per element and 32² elements, i.e. 128² spatial degrees of freedom. The high-order DGSEM uses the entropy-conserving split-form powered by the flux of Chandrashekar in the volume, and the HLLC flux at the element interfaces. Positivity is controlled by adding subcell FV where the positivity is not fulfilled with the amount needed. All FV discretizations use the HLLC flux at the element interfaces and at the subcell interfaces as well.  

The first results show the high-order DGSEM result, which is formally 4th order accurate for smooth problems:

The next result uses a subcell finite volume approximation on the LGL-subcell grid, directly, i.e. without spatial reconstruction (piecewise constant approximation). The result is very dissipative:

The last results show the improvement when using a piecewise linear reconstruction with monotonized-central slope limiter on the LGL-subcell grid. The reconstruction is inner-element only, as it does not use element neighbor information. Thus, at the very first and very last LGL subcell, no reconstruction is used. Still, the accuracy is recovered nicely by this simple modification of the subcell FV scheme: 

Snapshot: Single-Node Performance Comparison of Four Different Magnetohydrodynamics Codes

We compare the runtime performance of four different magnetohydrodynamics codes on a single compute node on the in-house high performance cluster ODIN. A compute node on ODIN consists of 16 cores. We run the ‘3D Alfven wave’ test case up to a fixed simulation time and measure the elapsed wall clock time of each code minus initialization time and input/output operations. For each run the number of cores is successively increased. This allows us to get insights into the scaling behavior (speedup gain wih increasing number of cores) on a single compute node. Furthermore we plot the performance index (PID) over the number of nodes which is a measure of throughput, i.e. how many millions of data points (degrees-of-freedom/DOF) per second are processed by the each code.

The four contestants are:

  • Flash [1] with Paramesh 4.0 and the Five-wave Bouchut Finite-Volume solver written in Fortran
  • Fluxo [2] an MHD Discontinuous Galerkin Spectral Element code written in Fortran
  • Trixi [3] an MHD Discontinuous Galerkin Spectral Element code written in Julia
  • Nemo an in-house prototype code providing a 2nd order monotonized-central MHD-FV scheme (MCFV) and a hybrid MHD Discontinuous Galerkin Spectral Element / Finite Volume scheme (DGFV) written in Fortran.

Trixi uses a thread-based parallelization approach while Flash, Fluxo and Nemo
use the standard MPI method. Furthermore, Nemo also provides OpenMP-based
parallelization.

[1] https://flash.uchicago.edu/site/
[2] https://github.com/project-fluxo/fluxo
[3] https://github.com/trixi-framework/Trixi.jl

Snapshot: Hybrid Discontinuous Galerkin / Finite Volume (DG/FV) simulation of the multicomponent Shock-Bubble Interaction Problem

Simulation of the Shock-Bubble Interaction Problem with a hybrid entropy-stable DG/FV method and Adaptive Mesh Refinement (AMR) using Trixi (https://github.com/trixi-framework/Tr…).

The simulation uses a multicomponent model and computes the spatial operator as a blend of a first-order subcell FV method and a fourth-order DG scheme on a squared domain.

New paper published: A Novel Robust Strategy for Discontinuous Galerkin Methods in Computational Fluid Mechanics: Why? When? What? Where?

In this paper we will review a recent emerging paradigm shift in the construction and analysis of high order Discontinuous Galerkin (DG) methods applied to approximate solutions of hyperbolic or mixed hyperbolic-parabolic partial differential equations (PDEs) in computational physics. There is a long history using DG methods to approximate the solution of PDEs in computational physics with successful applications in linear wave propagation, like those governed by Maxwell’s equations, incompressible and compressible fluid and plasma dynamics governed by the Navier-Stokes and the Magnetohydrodynamics equations, or as a solver for ordinary differential equations (ODEs), e.g., in structural mechanics. The DG method amalgamates ideas from several existing methods such as the Finite Element Galerkin method (FEM) and the Finite Volume method (FVM) and is specifically applied to problems with advection dominated properties, such as fast moving fluids or wave propagation. In the numerics community, DG methods are infamous for being computationally complex and, due to their high order nature, as having issues with robustness, i.e., these methods are sometimes prone to crashing easily. In this article we will focus on efficient nodal versions of the DG scheme and present recent ideas to restore its robustness, its connections to and influence by other sectors of the numerical community, such as the finite difference community, and further discuss this young, but rapidly developing research topic by highlighting the main contributions and a closing discussion about possible next lines of research.

Published in: https://www.frontiersin.org/articles/10.3389/fphy.2020.500690/abstract

Front. Phys. | doi: 10.3389/fphy.2020.500690

New paper submitted: A Split-Form, Stable CG/DG-SEM for Wave Propagation Modeled by Linear Hyperbolic Systems

We present a hybrid continuous and discontinuous Galerkin spectral element approximation that leverages the advantages of each approach. The continuous Galerkin approximation is used on interior element faces where the equation properties are continuous. A discontinuous Galerkin approximation is used at physical boundaries and if there is a jump in properties at a face. The approximation uses a split form of the equations and two-point fluxes to ensure stability for unstructured quadrilateral/hexahedral meshes with curved elements. The approximation is also conservative and constant state preserving on such meshes. Spectral accuracy is obtained for all examples, which include wave scattering at a discontinuous medium boundary.

Preprint available at: arXiv:2012.06510

New paper submitted: Stability of Discontinuous Galerkin Spectral Element Schemes for Wave Propagation when the Coefficient Matrices have Jumps

We use the behavior of the L2 norm of the solutions of linear hyperbolic equations with discontinuous coefficient matrices as a surrogate to infer stability of discontinuous Galerkin spectral element methods (DGSEM). Although the L2 norm is not bounded by the initial data for homogeneous and dissipative boundary conditions for such systems, the L2 norm is easier to work with than a norm that discounts growth due to the discontinuities. We show that the DGSEM with an upwind numerical flux that satisfies the Rankine-Hugoniot (or conservation) condition has the same energy bound as the partial differential equation does in the L2 norm, plus an added dissipation that depends on how much the approximate solution fails to satisfy the Rankine-Hugoniot jump.

Preprint available at arXiv:2011.11746

New paper submitted: A Sub-Element Adaptive Shock Capturing Approach for Discontinuous Galerkin Methods

In this paper, a new strategy for a sub-element based shock capturing for discontinuous Galerkin (DG) approximations is presented. The idea is to interpret a DG element as a collection of data and construct a hierarchy of low to high order discretizations on this set of data, including a first order finite volume scheme up to the full order DG scheme. The different DG discretizations are then blended according to sub-element troubled cell indicators, resulting in a final discretization that adaptively blends from low to high order within a single DG element. The goal is to retain as much high order accuracy as possible, even in simulations with very strong shocks, as e.g. presented in the Sedov test. The framework retains the locality of the standard DG scheme and is hence well suited for a combination with adaptive mesh refinement and parallel computing. The numerical tests demonstrate the sub-element adaptive behavior of the new shock capturing approach and its high accuracy.

Preprint available at arXiv:2011.03338.

Snapshot: A new approach for approximating conservation laws

A new approach for approximating conservation laws has been tested: instead of monitoring the changes of the means of a quantity within a certain volume over time like a finite volume procedure, this method mimics the behavior of simple solutions.

First the current state is split into waves w, each aligned along one of the eigenvectors of the Fluxjacobian and living on its own grid. Then the corresponding grids are being moved with their eigenvelocity and finally all waves w are being overlayed and normalized yielding the solution after one timestep.

The plots show the solution of isothermal Euler equations at Time T=0.0000 (initial condition) and T=0.0025 with N=40 gridpoints for each mesh.