Category Archives: Snapshot
Snapshot: Interaction of Jupiter’s moon Io with the Jovian magnetosphere
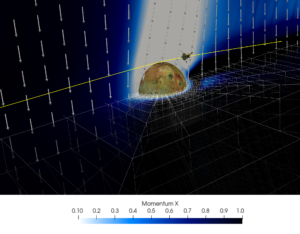
Io is the most volcanically active body of the solar system. Furthermore, it is embedded in Jupiter’s magnetic field, the largest and most powerful planetary magnetosphere of the solar system. Due to its strong volcanic activity, Io expels ions and neutrals, which are in turn ionized by ultraviolet and electron impact ionization, forming a plasma torus around Jupiter [1,2]. As Io moves inside the plasma torus, elastic collisions of ions and neutrals inside its atmosphere generate a magnetospheric disturbance that propagates away from Io along the background magnetic field lines at the Alfvén wave speed. This phenomenon creates a pair of Alfvén current tubes that are commonly called Alfvén wings, which have been observed by several flybys [1].
The figure shows the momentum (non-dimensional) and magnetic field of the plasma that surrounds Io, obtained with the magneto-hydrodynamic (MHD) plasma model of FLUXO*. The Alfvén wings can be observed as disturbances of both the background magnetic and momentum fields. In yellow is the trajectory of the I31 flyby of the Galileo spacecraft, which visited Io in 2001 [1]. The Galileo spacecraft is also depicted (not to scale). A 3D model of the moon’s surface developed by NASA [3] was superposed on the simulation results.
*FLUXO (www.github.com/project-fluxo/fluxo) is an MPI parallel high-order Discontinuous Galerkin code, which supports unstructured curvilinear hexahedral grids, and is able to perform Adaptive Mesh Refinement (AMR).
[1] M. Kivelson, K. Khurana, C. Russell, R. Walker, S. Joy, J. Mafi, GALILEO ORBITER AT JUPITER CALIBRATED MAG HIGH RES V1.0, GO-J-MAG-3-RDR-HIGHRES-V1.0, Technical Report, NASA Planetary Data System, 1997.
[2] J. Saur, F. M. Neubauer, J. E. P. Connerney, Plasma interaction of Io with its plasma torus, 2004.
[3] https://solarsystem.nasa.gov/resources/2379/io-3d-model/
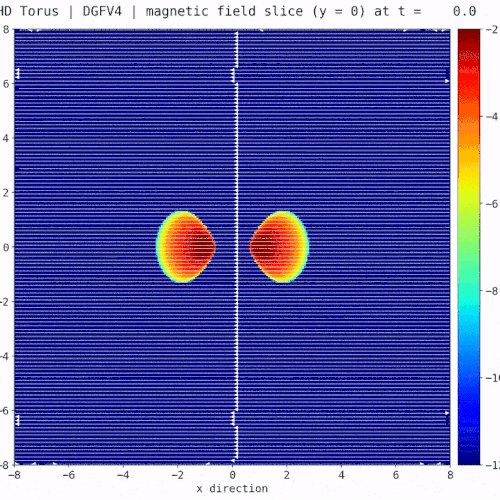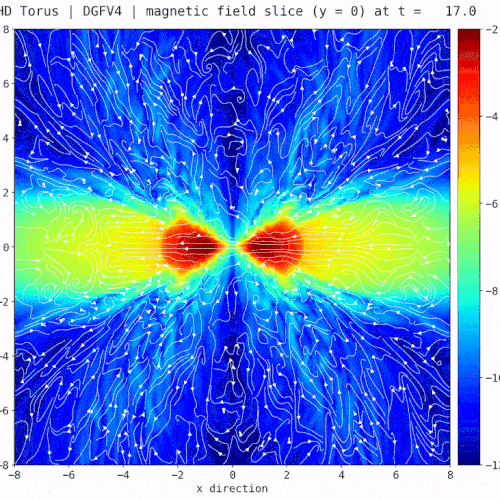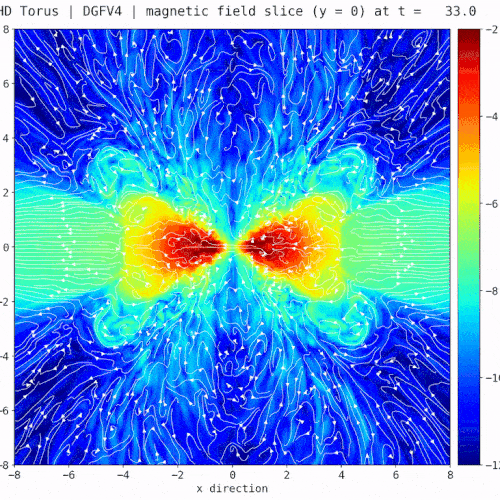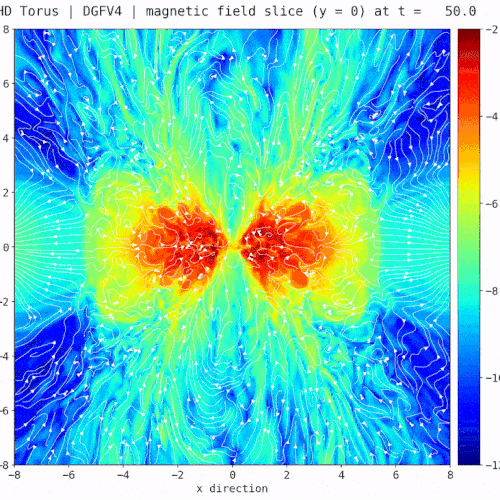
Snapshot: Evolution of a magnetized torus differentially rotating around a static point mass
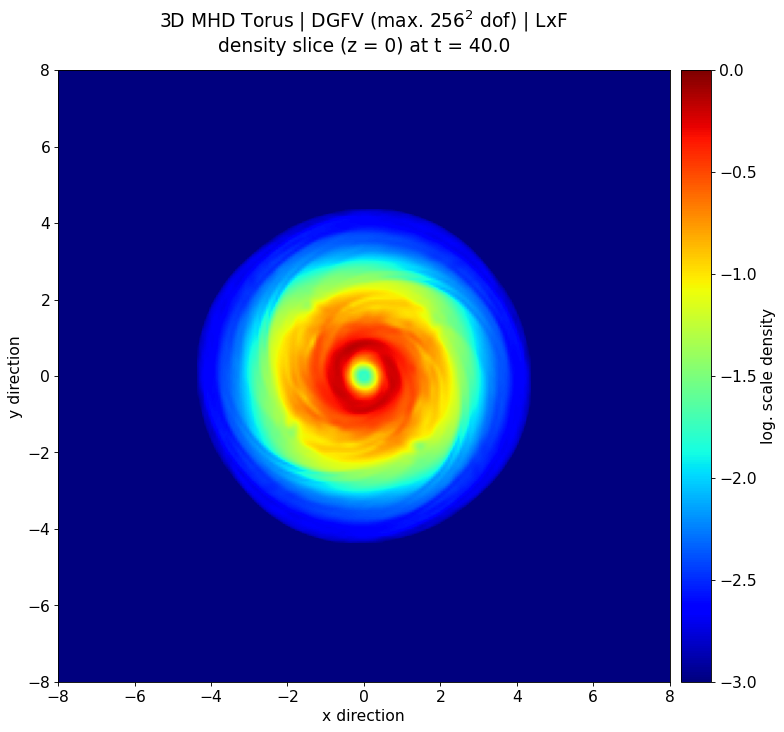
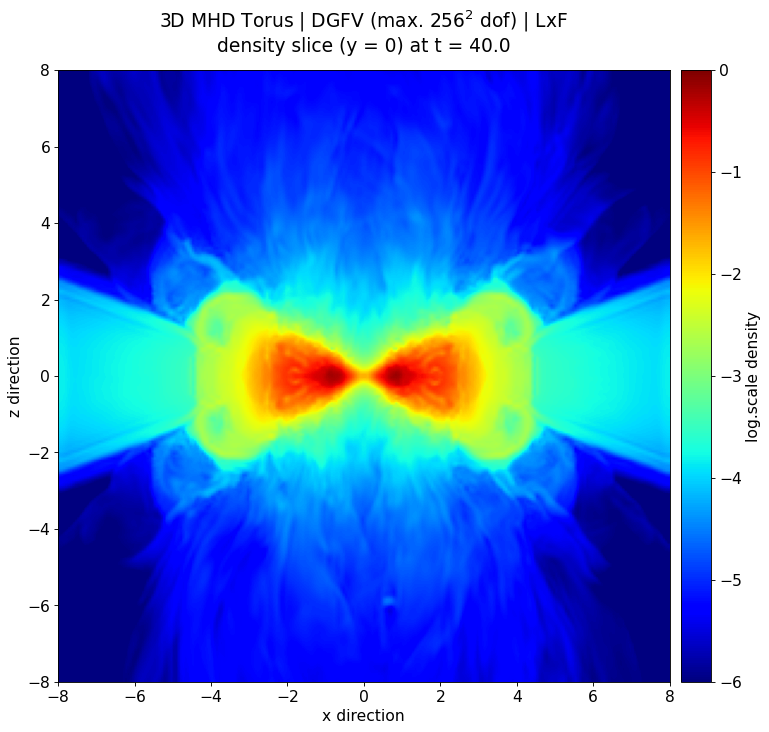
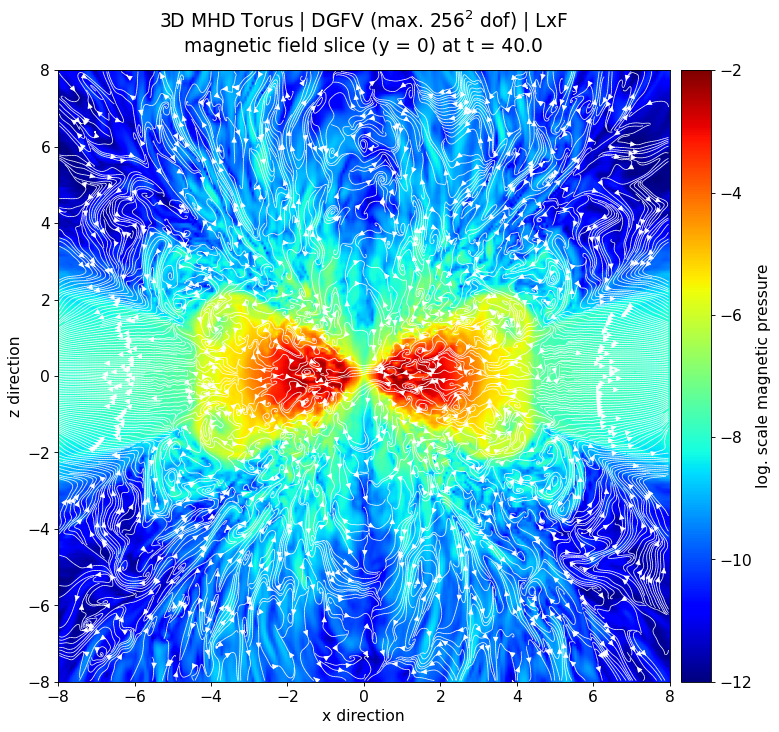
Evolution of a magnetized torus differentially rotating around a static point mass. [1] The torus gradually forms into an accretion disk with expanding filaments into the surrounding space due to magneto-rotational instabilities similar to the rich structure of the corona of our sun. The simulation was done with a new Discontinuous-Galerkin based MHD solver [2] in FLASH [3]. Fig. 1 and Fig. 2 show the log. scale density cross section in the x-y and x-z plane. Fig 3 highlights the rich structure of the magnetic field (white stream lines) overlayed on top of the log. scale magnetic pressure in the x-z plane.
[1] Machida, Mami, Mitsuru R. Hayashi, and R. Matsumoto.
“Global simulations of differentially rotating magnetized disks:
Formation of low-beta filaments and structured coronae.”
The Astrophysical Journal Letters 532.1 (2000): L67.
[2] Markert et al. “A Discontinuous Galerkin Method with Sub‑Cell Adaptive Shock Capturing for
FLASH” (in preparation)
[3] http://flash.uchicago.edu/
Snapshot: Gingerbread man simulation with unstructured quadrilateral elements
Here we are simulating a gingerbread man, whereby the gingerbread man itself has 861 unstructured quadrilateral elements. For the run parameters, we used polydeg = 10 with the compressible Euler equations and the manufactured (convergence test) solution. The visualization is done on nvisnodes=12 uniform points in each direction, on each element.

We thank Prof. Dr. Andrew Winters (https://liu.se/en/employee/andwi94) for providing this video/simulation.
Snapshot: Astrophysical colliding flow simulation run by a novel Discontinuous Galerkin/Finite Volume (DGFV) blending scheme in FLASH
Simulation of an astrophysical colliding flow [1] run by a novel Discontinuous Galerkin/Finite Volume (DGFV) blending scheme [2] which has been implemented in the FLASH code [3].
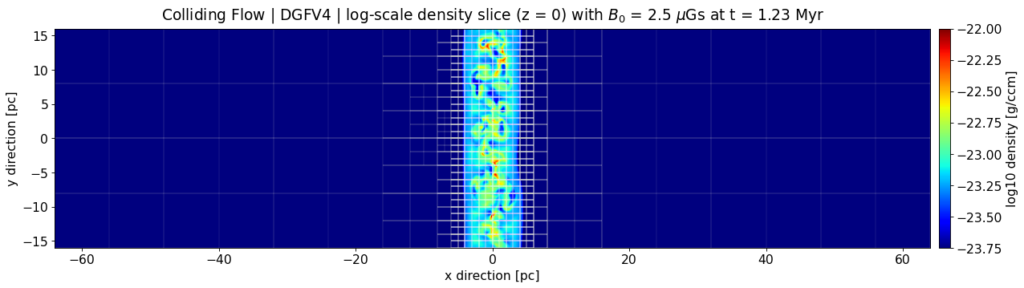
The code has following capabilities:
- fourth-order accurate ideal magneto-hydrodynamics with hyperbolic divergence cleaning [4]
- octree-based adaptive mesh refinement
- distributive computing and load balancing
- multi-species fluid dynamics (N_species > 10)
- turbulent driving
- octree-based Poisson solver for self-gravity [5]
- octree-based radiation physics [6]
- external gravitional fields
- sink particles [7]
- chemical reaction networks [8]
[1] Weis, Micheal et al. “The Virial Balance of CO-Substructures in Colliding Magnetised Flows” (in preparation)
[2] Markert, Johannes et al. “A Sub-Element Adaptive Shock Capturing Approach for Discontinuous Galerkin Methods” (submitted)
[3] Fryxell, Bruce, et al. “FLASH: An adaptive mesh hydrodynamics code for modeling astrophysical thermonuclear flashes.” The Astrophysical Journal Supplement Series 131.1 (2000): 273.
[4] Markert, Johannes et al. “Flash goes DG” (working title, in preparation)
[5] Wünsch, Richard, et al. “Tree-based solvers for adaptive mesh refinement code FLASH–I: gravity and optical depths.” Monthly Notices of the Royal Astronomical Society 475.3 (2018): 3393-3418.
[6] Wünsch, Richard et al. “Tree-based solvers for adaptive mesh refinement code FLASH – II: radiation transport module TreeRay” (submitted)
[7] Federrath, Christoph, et al. “Modeling collapse and accretion in turbulent gas clouds: implementation and comparison of sink particles in AMR and SPH.” The Astrophysical Journal 713.1 (2010): 269.
[8] Seifried, D., and S. Walch. “Modelling the chemistry of star-forming filaments–I. H2 and CO chemistry.” Monthly Notices of the Royal Astronomical Society: Letters 459.1 (2016): L11-L15.
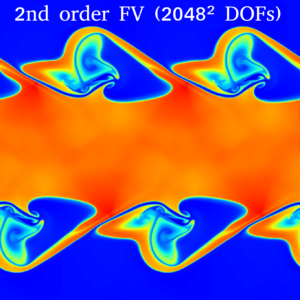
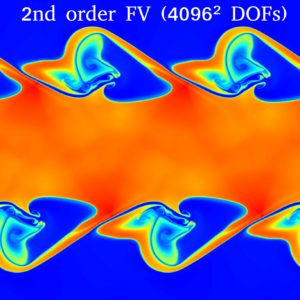
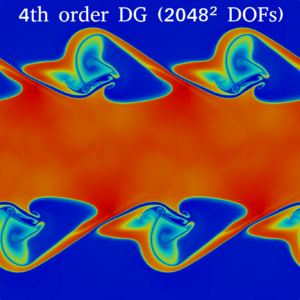
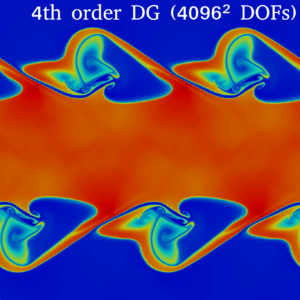
Snapshot: Simulation of a Kelvin-Helmholtz instability using second order Finite Volume schemes and fourth order Discontinuous Galerkin methods
We present in-viscid and viscous simulations of a Kelvin-Helmholtz instability using second a order accurate monotoniced-central finite volume (FV) method and a fourth order accurate discontinuous Galerkin (DG) method. The initial condition is given by [1]:
$$\rho (t=0) = \frac{1}{2}
+ \frac{3}{4} B,
~~~~~~~~~
p (t=0) = 1,~~~~~~~~~~
$$
$$
v_1 (t=0) = \frac{1}{2} \left( B-1 \right),
~~~~~~~
v_2 (t=0) = \frac{1}{10} \sin(2 \pi x),
$$
with $$B=\tanh \left( 15 y + 7.5 \right) – \tanh(15y-7.5).$$
We first present the FV results at end time $t=3.7$, which are computed using a monotoniced-central second order discretization of the Euler equations of gas dynamics on uniform grids.
The next results use a fourth order DG discretization of the Navier-Stokes equations on uniform grids using $Re=320.000$ at end time $t=3.7$. The highest resolution (4096² DOFs) is a direct numerical simulation (DNS) of the problem, where all scales are resolved.
It is remarkable that the numerical dissipation of the second order FV scheme causes the in-viscid simulation with 2048² DOFs to look very similar to the viscous DNS solution at $Re=320.000$.
[1] A.M. Rueda-Ramírez, G.J Gassner (2021). A Subcell Finite Volume Positivity-Preserving Limiter for DGSEM Discretizations of the Euler Equations. https://arxiv.org/pdf/2102.06017.pdf
Snapshot: Accuracy of the LGL-subcell FV scheme with and without inner-element reconstruction
We are interested in the accuracy of the finite volume scheme, on a LGL subcell grid induced by a LGL-DGSEM discretization. For comparison, we look at a Kelvin-Helmholtz-Instability test problem, simulated with 4² LGL nodes per element and 32² elements, i.e. 128² spatial degrees of freedom. The high-order DGSEM uses the entropy-conserving split-form powered by the flux of Chandrashekar in the volume, and the HLLC flux at the element interfaces. Positivity is controlled by adding subcell FV where the positivity is not fulfilled with the amount needed. All FV discretizations use the HLLC flux at the element interfaces and at the subcell interfaces as well.
The first results show the high-order DGSEM result, which is formally 4th order accurate for smooth problems:
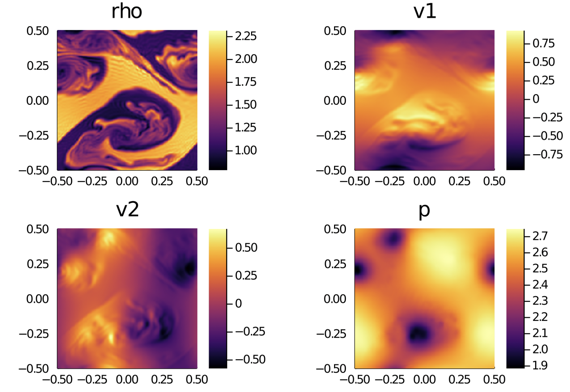
The next result uses a subcell finite volume approximation on the LGL-subcell grid, directly, i.e. without spatial reconstruction (piecewise constant approximation). The result is very dissipative:
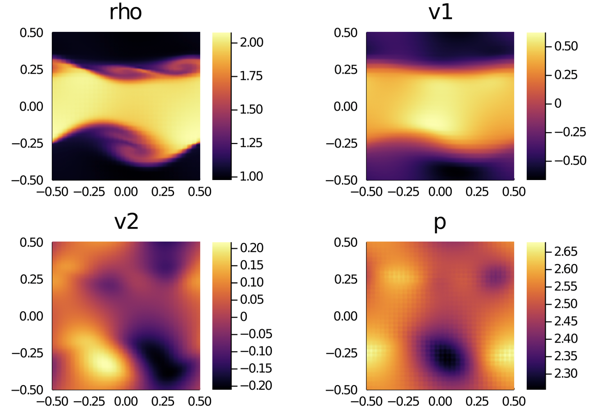
The last results show the improvement when using a piecewise linear reconstruction with monotonized-central slope limiter on the LGL-subcell grid. The reconstruction is inner-element only, as it does not use element neighbor information. Thus, at the very first and very last LGL subcell, no reconstruction is used. Still, the accuracy is recovered nicely by this simple modification of the subcell FV scheme:
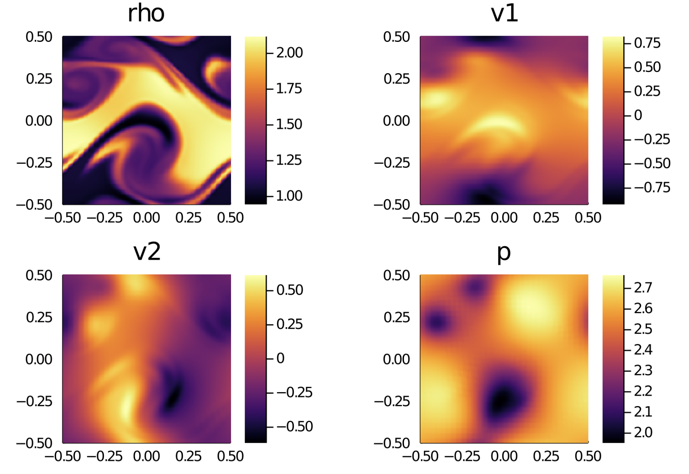
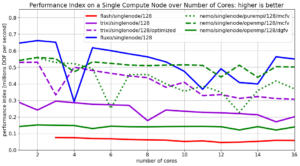
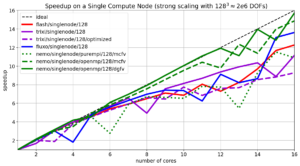
Snapshot: Single-Node Performance Comparison of Four Different Magnetohydrodynamics Codes
We compare the runtime performance of four different magnetohydrodynamics codes on a single compute node on the in-house high performance cluster ODIN. A compute node on ODIN consists of 16 cores. We run the ‘3D Alfven wave’ test case up to a fixed simulation time and measure the elapsed wall clock time of each code minus initialization time and input/output operations. For each run the number of cores is successively increased. This allows us to get insights into the scaling behavior (speedup gain wih increasing number of cores) on a single compute node. Furthermore we plot the performance index (PID) over the number of nodes which is a measure of throughput, i.e. how many millions of data points (degrees-of-freedom/DOF) per second are processed by the each code.
The four contestants are:
- Flash [1] with Paramesh 4.0 and the Five-wave Bouchut Finite-Volume solver written in Fortran
- Fluxo [2] an MHD Discontinuous Galerkin Spectral Element code written in Fortran
- Trixi [3] an MHD Discontinuous Galerkin Spectral Element code written in Julia
- Nemo an in-house prototype code providing a 2nd order monotonized-central MHD-FV scheme (MCFV) and a hybrid MHD Discontinuous Galerkin Spectral Element / Finite Volume scheme (DGFV) written in Fortran.
Trixi uses a thread-based parallelization approach while Flash, Fluxo and Nemo
use the standard MPI method. Furthermore, Nemo also provides OpenMP-based
parallelization.
[1] https://flash.uchicago.edu/site/
[2] https://github.com/project-fluxo/fluxo
[3] https://github.com/trixi-framework/Trixi.jl
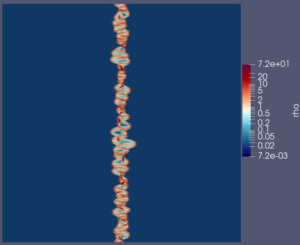
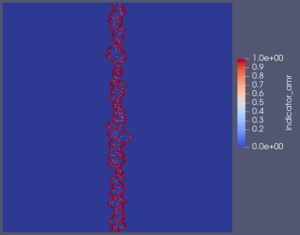
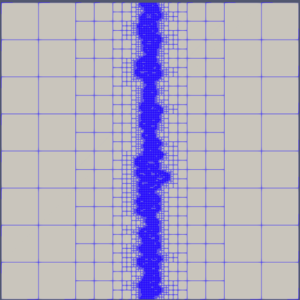
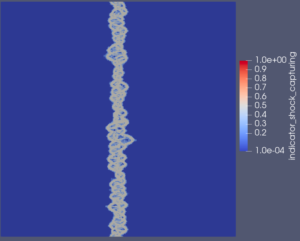
Snapshot: Hybrid Discontinuous Galerkin / Finite Volume (DG/FV) simulation of the multicomponent Shock-Bubble Interaction Problem
Simulation of the Shock-Bubble Interaction Problem with a hybrid entropy-stable DG/FV method and Adaptive Mesh Refinement (AMR) using Trixi (https://github.com/trixi-framework/Tr…).
The simulation uses a multicomponent model and computes the spatial operator as a blend of a first-order subcell FV method and a fourth-order DG scheme on a squared domain.
Snapshot: Hybrid Discontinuous Galerkin / Finite Volume (DG/FV) simulation of the Orszag-Tang vortex
Simulation of the Orszag-Tang vortex test with a hybrid entropy-stable DG/FV method and Adaptive Mesh Refinement (AMR) using FLUXO (https://github.com/project-fluxo/fluxo).
The simulation uses the GLM-MHD model to control div(B) errors and computes the spatial operator as a blend of a first-order subcell FV method and a fourth-order DG scheme.
The initial grid has 16×16 elements (64² DOFs), and the maximum resolution is achieved with three refinement levels (equivalent to 512² DOFs).