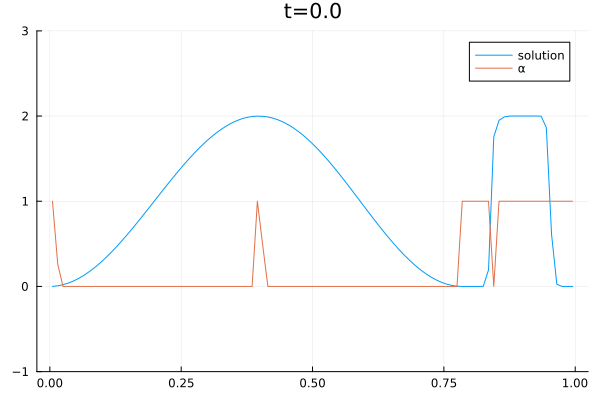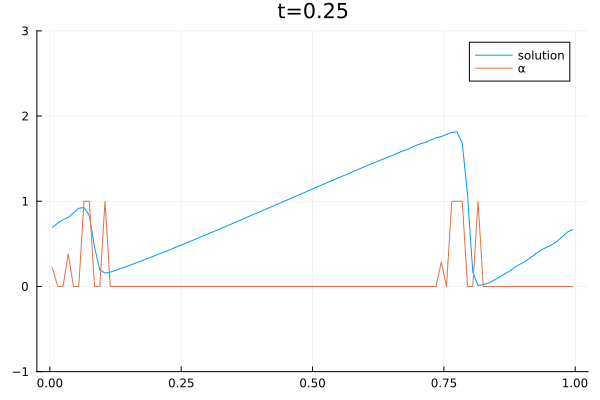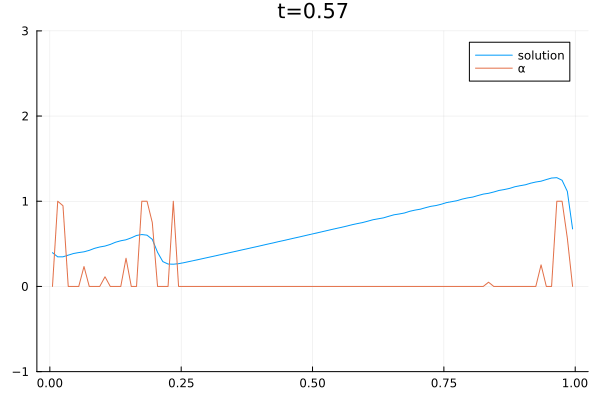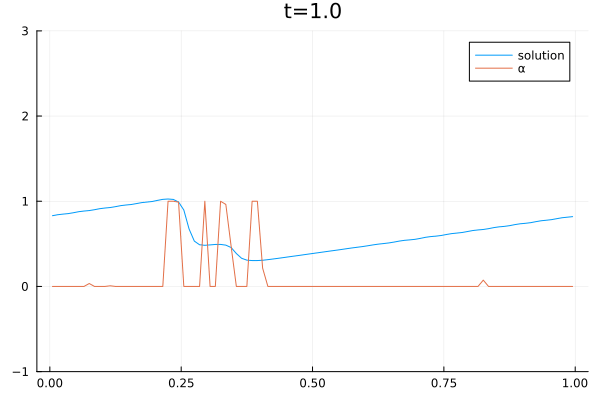
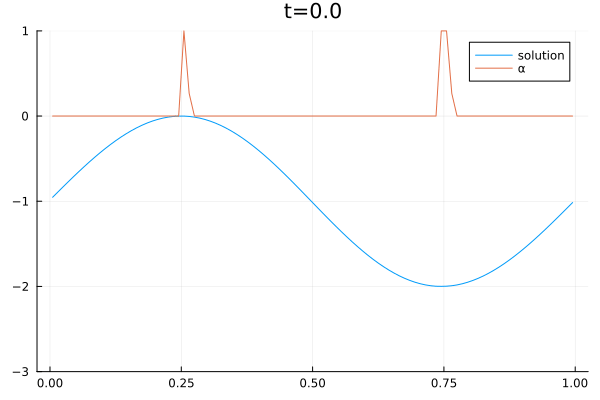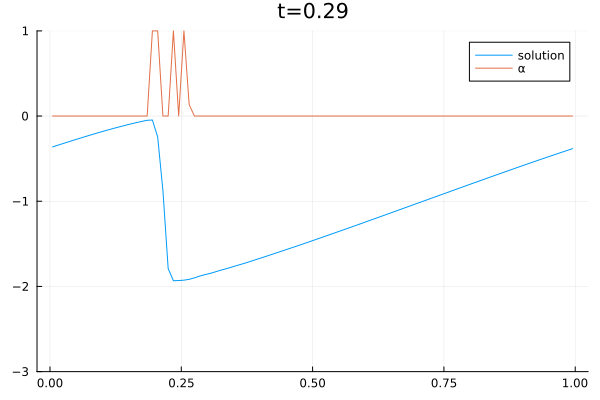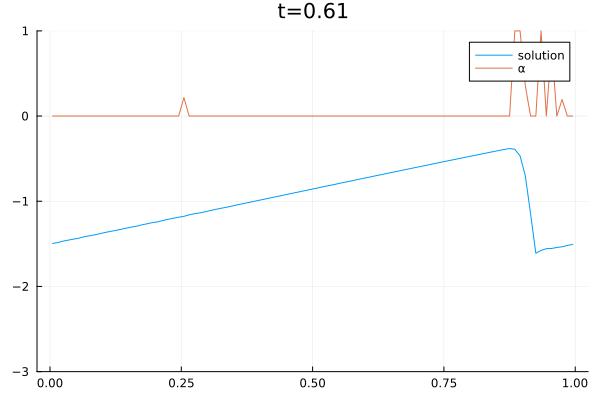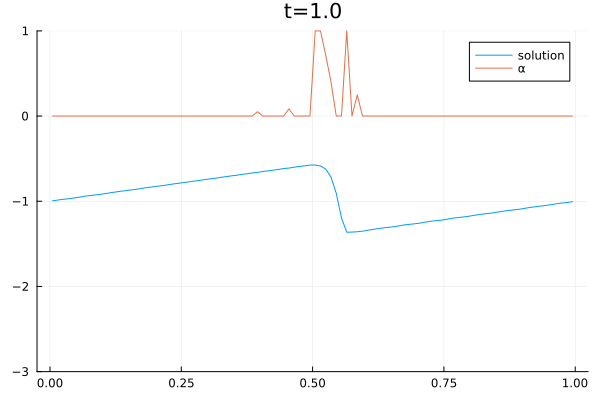
2D Sloshing simulation in a round tank oscillating from left to right. The simulation was done with the CFD code Trixi.jl [1] which was extended with a three-equations model [2]. The model consists of a two-phase flow simplification of the Baer–Nunziato equations of compressible multi-phase flows [3]. The shown simulation is part of combined research efforts of the German Aerospace Center (DLR) and the University of Cologne to create computational models of sloshing dynamics in liquid hydrogen storage systems on mobile platforms such as cars, ships, and planes.
References:
[1] https://trixi-framework.github.io/
[2] Dumbser, Michael. “A simple two-phase method for the simulation of complex free surface flows.” Computer methods in applied mechanics and engineering 200.9-12 (2011): 1204-1219.
[3] M.R. Baer, J.W. Nunziato: “A two-phase mixture theory for the deflagration-todetonation transition (DDT) in reactive granular materials”, J. Multiphase Flow 12 (1986) 861–889.
[4] Project HyTaZer: https://elib.dlr.de/201347/ and https://www.dlr.de/sy/PortalData/17/Resources/dokumente/wissenschaftstag/2022/6_Wissenschaftstag_2022_Hytazer_Freund.pdf
This Snapshot was created by Johannes Markert (http://jmark.de/).